Hajauttaminen on negatiivisen hinnan lounas
Markku Kurtti
Tässä keskustelunavaus ikivanhaan aiheeseen, mutta uudesta tulokulmasta.
Sijoittamisen kuuluisin fraasi lienee Markowitzin ”hajauttaminen on ilmainen lounas”. Ja miksi ei olisi, sillä Markowitz on oikeassa – kun puhutaan aritmeettisista tuotoista. Mutta suurin osa sijoittajista – varsinkin ne, jotka pyrkivät hyötymään ajan yli korkoa korolle ilmiöstä – eivät välitä aritmeettisesta vaan geometrisesta keskituotosta ja tuoton heilunnasta.
Kirjoitukseni lähtökohta on yksinkertaiseesti tämä: Jos sijoittaja mittaa sijoitusmenestystään portfolion geometrisilla tuotoilla aritmeettisten tuottojen sijaan, looginen johtopäätös on, että sijoittajan kannattaa arvioida hajauttamisen vaikutusta geometrisiin, ei aritmeettisiin, tuottoihin. Tässä tapauksessa Markowitzin malli ei täysin sovellu hajauttamisen hyötyjen tarkasteluun. Jos sijoittaja välittää ensisijaisesti aritmeettisista tuotoista, niin silloin Markowitzin malli on hänelle oikein hyvä.
Tästä eteenpäin oletan, että sijoittaja välittää geometrisesta tuotto-odotuksesta ja volatiliteetista.
Listaan heti tähän alkuun tärkeimmät johtopäätökset eli mikä hajauttamisen vaikutus on, kun sijoittaja välittää geometrisista tuotoista:
- Hajauttaminen ei ole ilmainen, vaan negatiivisen hinnan, lounas
- Geometrinen tuotto-odotus siis kasvaa hajautuksen lisääntyessä
- Heikosti hajauttava sijoittaja lähtee takamatkalta suhteessa täysin hajautettuun indeksiin.
- On väärin olettaa sama tuotto-odotus esim. 10 osakkeen portfoliolle kuin indeksille.
- USA:n osakedatassa Jan/1973 - Jun/2018 periodilla satunnaisesti poimittu 10 osakkeen ”equally weighted” kuukausittain rebalansoitu portfolio hävisi keskimäärin 1.6 prosenttiyksikköä indeksituotolle. Stock picker tarvitsi siis keskimäärin 1.6 prosenttiyksikkö taitoa, jotta pääsi takamatkalta tasoihin indeksin kanssa. Vasta tuon 1.6 prosenttiyksikköä ylittävä taito alkoi tuottaa ylituottoa.
- Osakepaino vaikuttaa hajautushyötyyn
- Pienellä osakepainolla hajauttamisen merkitys on pienempi, mutta suurella painolla hajauttamisesta saatava hyöty kasvaa valtavasti
- Etenkin jos aikoo vivuttaa osakesijoituksia niin hajauttamisesta tulee äärimmäisen tärkeää
- Sijoitustyyli vaikuttaa hajautushyötyyn
- Hajautushyötyyn vaikuttaa osakkeiden firmakohtainen (idiosynkraattinen) varianssi, joka vaihtelee merkittävästi eri tyylisten osakkeiden välillä
- Pienillä firmoilla hajautusta vaaditaan paljon enemmän kuin suurilla. Varsinkin microcap firmoilla heikko hajautus syö tuotto-odotusta isosti verrattuna täysin hajautettuun microcap-indeksiin. Megacapeilla hajautusta vaaditaan paljon vähemmän.
- Sijoitustyyleistä esim. korkean earnings yieldin omaavat osakkeet vaativat paljon vähemmän hajautusta kuin matalan earnings yieldin osakkeet. Lisäksi hajautushyötyero vastakkaisten tyylien välillä on ollut erittäin luotettava kuukaudesta ja vuodesta toiseen, toisin kuin tuottoero tyylien kesken.
Tarkempi teoria ja empiiriset tulokset löytyy täältä: http://urn.fi/URN:NBN:fi:oulu-202011203162
Yllä olevan linkin takaan löytyvä gradu ja sen sisältämä teoria geometrisen ja aritmeettisen tuoton eroista selittää suurelta osin kuuluisat tutkimustulokset, jotka perustuvat ajan yli realisoituneisiin (geometrisiin) tuottoihin aritmeettisten tuottojen sijaan. Esimerkiksi:
Bessembinder, H. (2018): Do stocks outperform Treasury bills?
J.P. Morgan: The Agony and the Ecstasy: The Risks and Rewards of a Concentrated Stock Position
Riskin eli volatiliteetin suhteen ei ole käytännössä eroa välittääkö sijoittaja geometrisista vai aritmeettisista tuotoista. Volatiliteetti pienenee molemmille tuotoille käytännössä samalla tavalla hajautuksen lisääntyessä eli hajauttaminen pienentää portfolion riskiä. Riskin pienentäminen onkin hajauttamisen ainoa funktio Markowitzin mallissa. Markowitzin mukaan hajauttaminen on ilmainen lounas, koska riski pienenee samalla kun (aritmeettinen) tuotto-odotus pysyy muuttumattomana hajautuksen lisääntyessä.
Riskin lisäksi sijoittajaa kiinnostaa tietysti tuotto-odotus. Geometrinen tuotto-odotus poikkeaa oleellisesti aritmeettisesta vastinparistaan siinä, että sen suuruus riippuu volatiliteetista. Mitä suurempi vola, sitä pienempi geometrinen tuotto-odotus. Tämä ilmiö tunnetaan esimerkiksi nimillä ”variance drain” tai ”volatility drag”. Hieman vähemmän tunnettua on, että osakepaino vaikuttaa ”variance drain” -komponenttiin neliöitynä. Alla geometrisen tuotto-odotuksen, g:n, kaava:
g = r + f*(m-r) - f^2*(s^2/2) (kaava 14 gradussa)
r = riskitön korko
m = portfolion aritmeettinen tuotto-odotus
f = osakepaino (”investment fraction”)
s = portfolion volatiliteetti (jolloin s^2 on portfolion varianssi)
Hajauttaminen ei vaikuta aritmeettiseen tuotto-odotukseen (m), mutta pienentää volatiliteettia (s), jolloin kaavasta nähdään, että geometrinen tuotto-odotus (g) kasvaa kun hajauksen määrä kasvaa. Samoin nähdään, että volatiliteetti alkaa pienentää g:tä voimakkaasti, kun osakepaino ylittää 100% (f>1).
Testasin kyseistä g:n kaavaa (tarkalleen ottaen g-r) USAn historiallisilla osaketuotoilla (CRSP datalla) aikavälillä Jan/1973 – Jun/2018 eli 45.5 vuoden periodilla. Kyseinen periodi sisältää kuukausituotot kaikkille USAn osakkeille (keskimäärin 5472 osaketta per kuukausi). Muodostin portfoliot (50 000 kpl) kuukausittain satunnaisesti tasapainoin (”equally weighted”) ja kuukausittain rebalansoiden. On hyvä huomata, että microcap osakkeet dominoivat tuloksia. Alla olevassa kuvassa nähdään keskimääräinen geometrinen ”risk premium” (geometrinen keskiarvotuotto miinus riskittömän koron tuotto) eli nollakohta on riskittömän koron annualisoitu tuotto. Kaikki tuotot ovat continuous compounding muodossa. ”Bootstrapped” on empiirisestä datasta mitattu arvo kun ”Predicted” on kaavan ennustama arvo. X-akselina on sijoitusaste (f=1 vastaa 100% osakeallokaatiota ja se mikä ei ole osakkeissa on riskittömässä korossa). Kuvasta nähdään kuinka portfolion geometrinen tuotto-odotus kasvaa hajautuksen kasvaessa. Samoin nähdään, että geometrisella tuotolla (toisin kuin aritmeettisella) on maksimiarvo sijoitusasteen funktiona (esim. täysin hajautetun benchmark-indeksin maksimi saavutetaan ns. full Kelly -pisteessä hieman yli 200% sijoitusasteella, kun se yhden osakkeen portfoliolla saavutetaan jo 29% sijoitusasteella). Kuvasta nähdään myös, että 100% sijoitusasteella yhden osakkeen portfolion risk premium jää keskimäärin noin 7 prosenttiyksikköä alle riskittömän koron (mikä omalta osaltaan vastaa Bessembinderin kysymykseen ”Do stocks outperform Treasury bills?”).
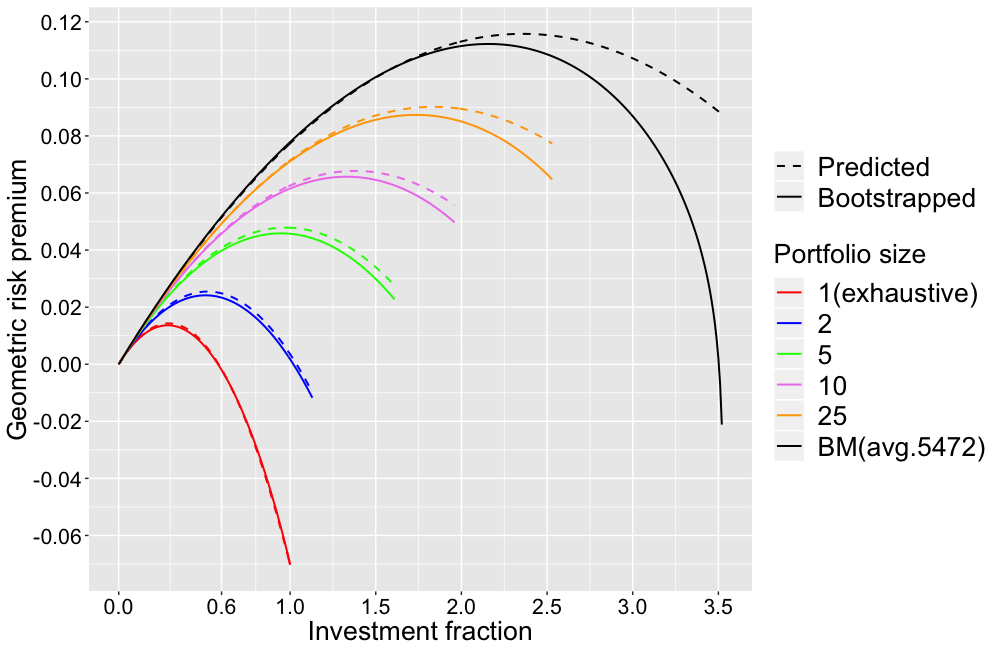
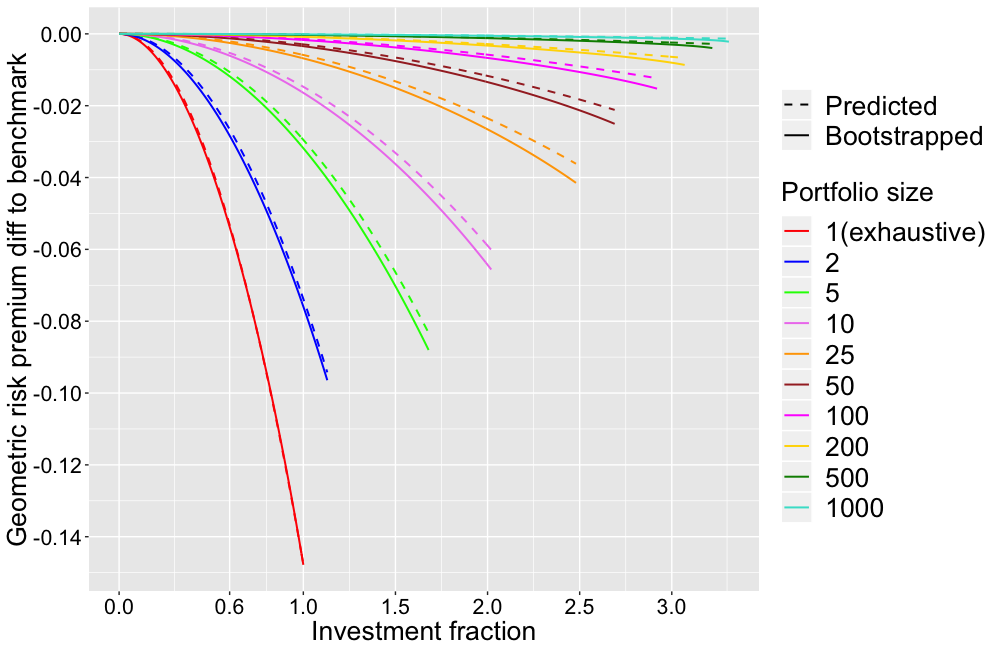
Hajautuksen vaikutus nähdään selvimmin, kun vähennetään portfolion geometrisesta risk premiumista täysin hajautetun benchmark portfolion vastaava. Tämä geometristen tuotto-odotusten erotus näkyy seuraavassa kuvassa. Kuvasta nähdään miten hajautuksen vaikutus kasvaa rajusti kun sijoitusaste kasvaa. 100% sijoitusasteella yhden osakkeen portfolio häviää keskimäärin lähes 15 prosenttiyksikköä täysin hajautetulle benchmark-indeksille kun 10 osakkeen portfolio häviää noin 1.6 prosenttiyksikköä.
”Benchmark Diversification Premium” (DP) tarkoittaa benchmark-indeksin ja 1 osakkeen portfolion geometrisen keskituoton erotusta (nyt noin 15 prosenttiyksikköä). Tämä kuvaa hajautuksesta saatavan tuotto-odotushyödyn maksimia ja saadaan kaavasta:
DP = (IVar/2)*f^2 = DP(f=1)*f^2 (kaava 38 gradussa)
IVar = keskimääräinen 1 osakkeen idiosynkraattinen varianssi
f = osakepaino
DP(f=1) = Benchmark Diversification Premium 100% osakepainolla
ja n-osakkeen portfolion geometrisen keskituoton ero täysin hajautettuun benchmark-indeksiin (delta_DP) voidaan approksimoida kaavalla:
delta_DP = -DP/n = -(DP(f=1)/n)*f^2 (kaava 42 gradussa)
n = portfolion osakkeiden lukumäärä
Eli 100 osakkeen portfolio häviää noin 0.15 prosenttiyksikköä indeksille (-15/100 = -0.15). Tämä kuvastaa kuinka hajauttaminen on negatiivisen hinnan lounas geometrisille metriikoille (kuten geometrinen tuotto-odotus tai geometrinen risk premium). Samalla kuva näyttää miltä takamatkalta stock picker lähtee voittamaan indeksiä. Esimerkiksi 200% sijoitusasteella vivuttava stock picker antaa 10 osakkeen portfolioilla yli 6 prosenttiyksikön ((-15/10)*2^2 = -6) etumatkan indeksille.
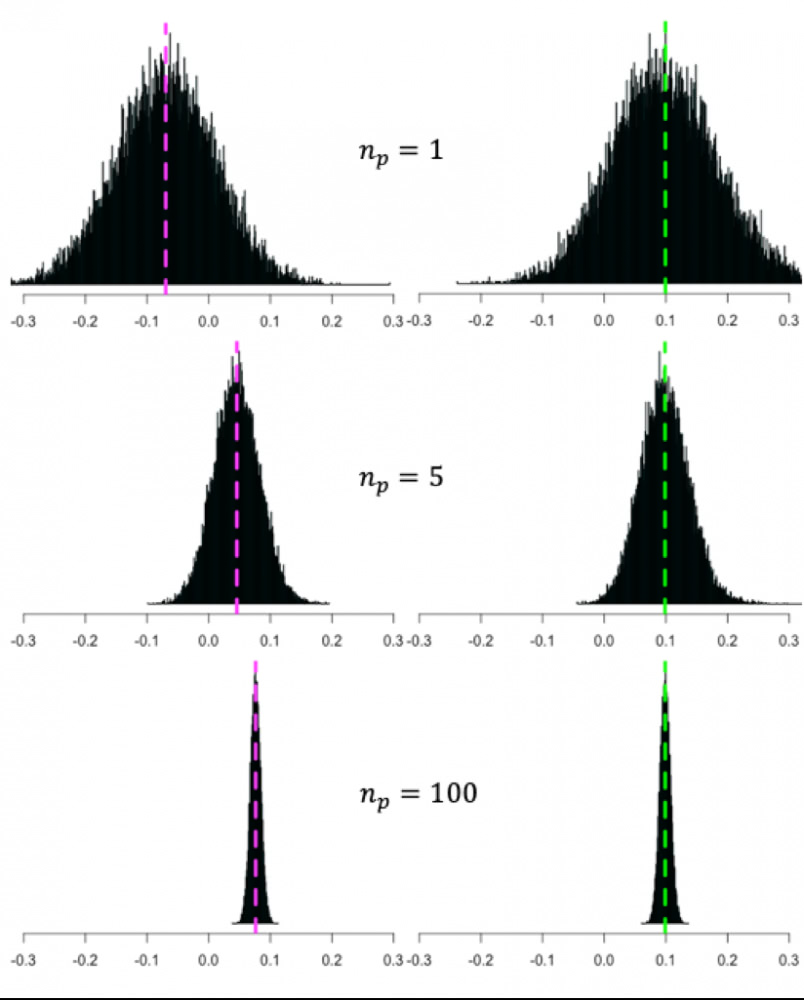
Alla vielä kuva, joka havainnollistaa geometristen (vasemmalla) ja aritmeettisten tuottojen (oikealla) eroa hajautuksen funktiona. Kuva on empiirisestä datasta (sama data kuin aikaisemminkin) josta on poimittu satunnaisesti 20 000 kpl portfolioita kuukausittain ja linkitetty tuotot 45.5 vuoden periodilta. Portfolio-kokoja on kolme: 1, 5 ja 100 osaketta. Geometrisilla tuotoilla mitattuna portfolioiden annualisoitu tuottojakauma (ja keskiarvotuotto) liikkuu oikealle (tuotto kasvaa) kun hajautusta lisätään. Aritmeettisilla tuotoilla mitattuna keskiarvotuotto pysyy vakiona. Molemmilla tuotoilla jakauma kapenee (riski pienenee) kun hajautusta lisätään. Vasemmalla näemme siis, kuinka hajauttaminen tarjoaa negatiivisen hinnan lounaan, kun oikealla lounas on ”vain” ilmainen. Lisäksi kuvasta nähdään, että hyvälläkin (myös täydellä) hajautuksella geometrinen keskiarvotuotto jää noin 2 prosenttiyksikköä alemmalle tasolle kuin aritmeettinen keskiarvotuotto. Tämä ero tulee markkinaportfolion varianssista (systemaattinen riski) jota ei voida hajauttaa pois.
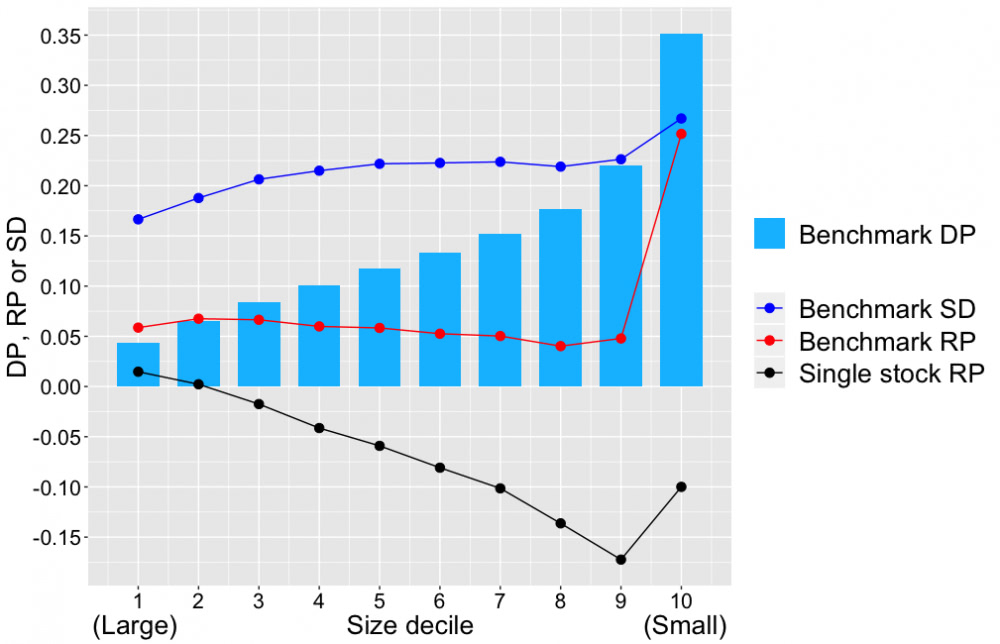
Sijoitustyylillä on suuri merkitys hajautuksen vaikutukselle tuotto-odotukseen. Kuva alla näyttää ”benchmark diversification premium” (DP) metriikan suuruuden firman koon mukaan. Voimme benchmark DP-metriikan avulla approksimoida hajautushyödyn mille tahansa portfolio-koolle edellä annetulla delta_DP kaavalla. Kuvasta nähdään, että hajautushyöty kasvaa firman koon pienentyessä. Suurimman desiilin firmoille 1 osakkeen portfolio häviää keskimäärin noin 5 prosenttiyksikköä (eli 10 osakkeen portfolio häviää noin 5/10=0.5 prosenttiyksikköä) indeksilleen. Pienimmän desiilin firmoille vastaavat luvut ovat 35 prosenttiyksikköä (ja 3.5 prosenttiyksikköä). Ero on 7 kertainen eli pienimmän desiilin firmat vaativat 7 kertaa enemmän hajautusta kuin suurimman desiilin firmat, jos halutaan pitää tuotto-odotustappio indeksille samalla tasolla. Jos pienimmät microcap yhtiöt joukkona ovatkin epätehokkaimmin hinnoiteltuja, niin vastapainona heikosti hajautettuna osa siitä epätehokkuuden suomasta tuotto-odotusedusta hävitään antamalla iso etumatka indeksille.
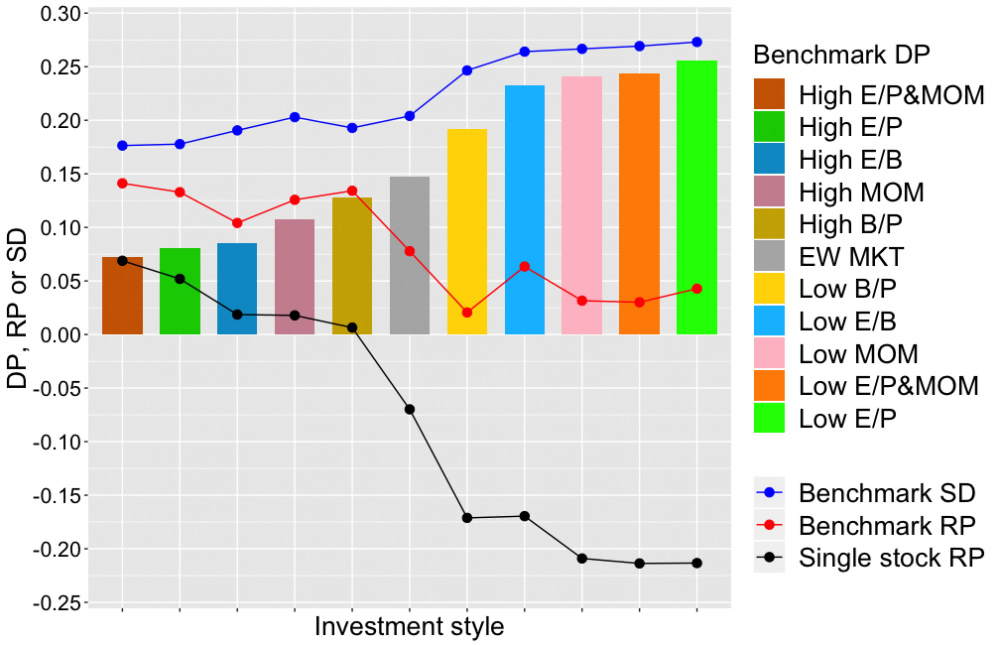
Seuraavassa kuvassa katsotaan tarkemmin erilaisia sijoitustyylejä. Keskellä on referenssinä tyylitön tasapainoin rakennettu markkinaportfolio (EW MKT). Vähiten hajautuksesta hyötyy (tai vähiten hajautusta vaatii) high earnings yield osakkeet joilla on lisäksi hyvä momentum (High E/P&MOM). 10 osakkeen portfolio häviää indeksilleen keskimäärin 0.7 prosenttiyksikköä. Eniten hajautusta vaativa tyyli on low earnings yield, jonka 10 osakkeen portfolio häviää indeksilleen yli 2.5 prosenttiyksikköä. Mielenkiintoisesti historiallisesti hyvin indeksitasolla tuottaneet tyylit (joilla korkea Benchmark RP kuvassa) ovat vaatineet myös vähiten hajautusta. Single stock RP kuvassa kertoo mikä on ollut 1 osakkeen portfolion geometrinen risk premium (RP). Paljon hajautusta vaativilla tyyleillä se on todella heikko, luokkaa -20 prosenttiyksikköä. Näillä tyyleillä on hävitty riskittömälle korolle ihan huolella, kun vähän hajautusta vaativilla tyyleillä on aina keskimäärin voitettu riskitön korko jo 1 osakkeen portfoliokoolla. Tässä kohtaa vastaus Bessembinderin kysymykseen ”Do stocks outperform Treasury bills?” olisi “depends on your investing style”.
Yhteenveto
Geometrisesta tuotosta välittävälle sijoittajalle hajauttaminen on vielä tärkeämpää kuin perinteinen finanssiteoria antaa ymmärtää, koska hajauttaminen ei pelkästään alenna riskiä vaan lisäksi nostaa tuotto-odotusta.
Perinteinen finanssiteoria ei tarjoa työkaluja ymmärtää osakepainon merkitystä ja siihen liittyvää riskiä. Erityisesti vivuttamisen riski tulee esille, kun tarkastellaan osakepainon ja hajauttamisen vaikutusta geometrisiin keskiarvotuottoihin aritmeettisten keskiarvotuottojen sijaan.
Osakepoimijoille voi olla hyödyllistä ymmärtää eri sijoitustyylien suuret hajautusvaatimuserot kun hajautushyötyä mitataan portfolion geometrisen tuotto-odotuksen erona täysin hajautetun indeksin vastaavaan.

