big bad bear kirjoitti:

Hei, kirjoituksesi ovat peukutuksissa ja vastauksissa mielestäni aliarvostettuja. Kiitos vaivannäöstä ja kirjoituksista!

Kiitos kannustuksesta!

Ymmärrän kyllä, että tällaiset teoreettiset kirjoitukset kiinnostavat melko harvoja ja ehkä pitkä tutkimusraporttityylinen juttu ei ole houkuttelevin keskustelunavauksena.

Toisaalta minulla on myös hieman itsekäs motiivi kirjoittaa näitä juttuja. Yleensä opiskelen kirjoitukseen liittyvän aihepiirin samalla kun kirjoitan jutun. Kirjoittaminen taas pakottaa opiskelemaan ja jäsentämään asian peremmin ja ilmaisemaan sen jotenkin ymmärrettävästi. Eli samalla tulee itse opittua paljon.

Terve Jarkko. Kiitos mielenkiintoisesta kirjoituksesta. Ja kiitos gradun ja sen aiheen nostosta.

Mukava lukea, kun joku jaksaa kirjoittaa portfolion rakentamisesta, vaikka se ei ole ihan niitä kuumimpia aiheita nykyisessä sijoituskeskustelussa. Itse tykkään, että asiassa kuin asiassa perusteet on tärkeimpiä ja salkun rakentaminen, jos joku, on sijoittamisen perusta. 

Kirjoituksessasi ja siihen liittyvässä blogikirjoituksessa oli useita yhtymäkohtia omiin mielenkiinnonkohteisiini sijoittamisessa. Mainitsit S-käyrän liittyen sijoittajien drawdown-sietokykyyn ja puhuit siitä, miten ei kannata pelata (eli sijoittaa riskiseen portfolioon ainakaan suurella painolla) jos on jo voittanut pelin (eli saavuttanut sijoitustavoitteensa tai merkittävän osan siitä). Molemmat ajatukset löytyvät William Bernsteinin tuotannosta ja Bernstein onkin yksi omista suosikkikirjoittajistani sijoittamiseen liittyen. Bernsteinin yksi lempiajatus on myös, että toimiva epäoptimaalinen strategia on parempi kuin ei toimiva optimaalinen strategia. Eli lopulta ratkaisevaa on mikä toimii kenellekin ja tuotot teoriassa maksimoiva strategia ei usein ole paras mahdollinen valinta. Ylimääräinen volatiliteetti, vaikka jotkut sitä voivat sietää paljonkin, on varmuudella asia mikä suurimalle osalle ihmisistä (ja heidän sijoitusstrategian onnistumisen kannalta) on haitallista.

On aika yleinen ajatus, että koska riski ja tuotto kulkevat käsi kädessä, niin mikä tahansa riskinotto kannattaa, kun vaan jaksaa odottaa ja sietää lyhyen aikavälin volatiliteettia. Puhuitkin kirjoituksessasi systemaattisen (kompensoidun) ja epäsystemaattisen (kompensoimattoman) riskin erosta. Paras intuitiivinen kuvaus mikä olen kuullut näiden kahden riskin erosta, on MIT professorilta Andrew Lo:lta. Se meni suunnilleen näin: Lo kertoi nähneensä joskus New Yorkin hotellissa 30. kerroksessa ikkunan ulkopuolella ikkunanpesijän ja ajatelleensa, että tuo on riskialtis ammatti eli palkassa pitäisi olla jonkinlainen riskilisä. Lo oli tarkistanut palkkatilastoista, että korkeiden rakennusten ikkunanpesijöillä on keskimäärin korkeat palkat koulutustasoonsa ja työn vaativuuteen nähden eli työnantajat maksavat riskistä. Mutta Lo tarjosi ajatuskokeen: jos yksi ikkunanpesijöistä ikkunoita pestessään samalla tanssii ripaskaa tellingeillään, hänen riskitasonsa varmasti nousee, mutta maksaako työnantaja hänelle korkeampaa palkkaa nyt kun riski on korkeampi? Ei tietenkään maksa, koska ikkunanpesijän ei tarvitset ottaa ripaskariskiä työnsä suorittamiseksi vaan se on hänen oma valintansa. Samalla tavalla sijoittajan ei tarvitse ottaa ylimääräistä epäsystemaattista riskiä, joka on hajautettavissa, eikä hänelle makseta korvausta vapaaehtoisen riskin kantamisesta.

Toinen pointti kompensoimattomaan riskiin liittyen on, että se mikä on kompensoimatonta (”uncompensated risk”) riskiä aritmeettisten tuottojen maailmassa on maksullista riskiä (”costly risk”) geometristen tuottojen maailmassa eli käytännön korkoa-korolle sijoitusmaailmassa. Eli, kuten demonstroit historiallisten tuottojen avulla, CAGR kasvaa, kun kompensoimatonta eli hajautettavissa olevaa riskiä hajautetaan pois. Epäsystemaattinen riski on siis maksullista koska se pienentää CAGRia. Tämän vuoksi esimerkiksi heikosti hajauttava osakepoimija lähtee takamatkalta indeksirahastoon verrattuna ja osakepoimintataidosta (mikäli sellaista on) osa menee takamatkan saavuttamiseen. Koska suurimmalla osalla ei ole osakepoimintataitoa, selittää tämä ilmiö omalta osaltaan sitä, että heikosti hajauttavat osakepoimijat jäävät pitkällä aikavälillä yleensä alle indeksituoton.

Puhut paljon riskikorjatusta tuotosta pelkän tuoton sijaan ja se onkin erityisen tärkeää, kun puhutaan geometrisista tuotoista. Olen viime aikoina tutkinut paljon nimenomaan geometrista tuottoa ja sen kannalta näyttää olevan kolme oleellista parametria: sijoitusaste, volatiliteetti ja Sharpe ratio. Näiden kolmen avulla voidaan määrittää hyvin pitkälti portfolion odotettu kasvunopeus (eri sijoitusasteilla) ja myös riskiin liittyviä metriikoita kuten drawdown. Riskikorjattu tuotto (Sharpe ratio) on keskiössä ja putkahtaa esille aina kun puhutaan geometrisista tuotoista. Tutkin hetki sitten enemmän drawdown-riskiä. Tarkemmin sanottuna maksimi-drawdownin (portfolion nykyarvosta) odotusarvoa. Myös tämä metriikka paljastui riippuvan sijoitusasteesta, volatiliteetista ja Sharpe ratiosta. Koska drawdown-riski aiheena liippaa läheltä näitä sinun kirjoituksiasi, niin tässä linkki aiheeseen.

Myös minua kiinnostaa eri omaisuusluokat (sisältäen osakefaktorit) osakkeiden lisäksi. Näihin en ole ehtinyt vielä syventyä niin paljoa kuin toivoisin. Odotankin mielenkiinnolla seuraavaa kirjoitustasi näihin liittyen.

Mesut Özil kirjoitti:

Jos salkun X sharpe = 3 ja markkinat romahtaa, niin mukanahan menee myös hyvän sharpen portfolio ja drawdown toteutuu isosti muun paniikin mukana.

Ymmärrän pointin. Osakkeiden keskinäiset korrelaatiot tunnetusti lähestyvät ykköstä, kun markkinalla tulee iso romahdus. Tämä on aito ongelma osakemarkkinan sisällä hajauttamisen ja Sharpen maksimoinnin kannalta.

Tästä päästäänkin aiheeseen, jota en kirjoituksessani käsitellyt. Miten Sharpe maksimoidaan? Sharpe maksimoidaan muodostamalla portfolio keskenään korreloimattomista (tai vähän korreloivista) asseteista. Tämä voi tarkoittaa periaatteessa mitä vaan assetteja: osakkeet (osakemarkkinariski), korot, kiinteistöt, kulta, raaka-aineet, osakemarkkinan eri faktorit, kryptot jne. Pointti on, että Sharpea ei voi maksimoida pelkästään osakkeisiin sijoittamalla. Bonuksena eri omaisuusluokkiin sijoittaminen voi lieventää kirjoituksessa käsiteltyä momentum-ongelmaa ja siten tuoda empiiristä drawdown-riskiä lähemmäs teoreettista ennustetta.

Myös rahoitusteoria olettaa, että markkinaportfolio (jonka oletetaan maksimoivan Sharpe) sisältää kaikki maailman assetit, ei pelkästään osakkeita. Kirjoituksessani testasin teoriaa empiirisesti vain osakemarkkinan sisällä, koska sieltä on dataa paljon ja helposti saatavilla.

Toki Sharpen maksimointi eli käytännössä hajauttaminen auttaa myös osakemarkkinan sisällä. Tuo minun drawdown-riski metriikka on odotusarvo maksimi drawdownille portfolion nykyarvosta (tai riskittömästä tuotosta). Tämä on eri asia kuin drawdown portfolion edellisestä huipusta. Tuon minun metriikan kannalta on olennaista tuleeko markkinaromahdus huomenna vai kymmenen vuoden päästä. Kymmenen vuoden päästä, jos portfolion arvo on tuplaantunut niin -50% markkinaromahdus ei aiheuta drawdownia alkupääomasta mitattuna. Todennäköisyys isolle markkinaromahdukselle huomenna tai seuraavan vuoden aikana on hyvin pieni. Siksi markkinaromahdukset eivät vaikuta maksimi drawdownin odotusarvoon niin paljoa kuin voisi kuvitella. 

Täällä on SP500 drawdownit (edellisestä huipusta) noin 150 vuoden ajalta. Suuri, yli 40% romahdus (joskin kuukausidatasta) on tapahtunut 6 kertaa eli noin kerran 25 vuodessa. 25 vuoden aikana heikosti hajautettu portfolio ehtii tehdä keskimäärin monta suurta drawdownia puhtaasti hajauttamattoman (epäsystemaattisen eli markkinan kanssa korreloimattoman) riskin voimin. Minun empiirisessä testissä 10 vuoden periodilla (liukuvalla aloituspäivällä) maksimi drawdownin keskiarvoksi tuli 23.8%. Tämä siitä huolimatta, että heinäkuussa 1932 markkina (tuotto yli riskittömän koron) pohjasi (päivittäisestä datasta mitattuna) -84.8% lukemaan edellisestä huipusta. Yksittäinen suuri mutta harvinainen tapahtuma ei määritä odotusarvoa.

Niinä ajanhetkinä (eli harvoin) kun osakemarkkina (suuren Sharpen portfolio) romahtaa niin kaikki osakeportfoliot romahtavat. Niinä ajanhetkinä (suurimman osan ajasta) kun markkina ei romahda, niin heikosti hajautetut (pienen Sharpen) portfoliot romahtelevat tämän tästä. Keskiarvona (odotusarvona) pienen Sharpen portfoliot romahtelevat alkuarvostaan siis enemmän.

Jos todellinen musta joutsen iskee ja nollaa osakemarkkinat niin silloin tietty osakkeiden sisällä hajauttaminen ja Sharpen maksimointi ei paljoa lämmitä. Siinäkin tapauksessa omaisuusluokkien yli hajauttaminen voi tuoda liennytystä (suola, sokeri, säilykkeet, polttoaineet, ammukset?).

Juha X kirjoitti:

Kysymykseni rebalanssoinnista ja sijoitustyylistä heräsi siitä, että rebalanssointi takaisin saman salkun alkuperäisiin tasapainotuksiin ei empiirisesti välttämättä ole tehokkain tapa kasvattaa varallisuutta

Olen samaa mieltä, että käytännössä tuo minun tutkimuksessa käyttämä kuukausittainen rebalansointi tasapainoihin ei ole mikään tyypillinen tapa. Oikeassa elämässä kun myös kulut vaikuttavat kuten myös se, että moni sijoittaja ei jaksa joka kuukausi olla painoja säätämässä. 

Lisäksi yksinkertaisiin malleihin verrattuna todellisuus on monimutkaisempi. Esimerkiksi momentum voi olla hyödyllistä ottaa huomioon rebalansoinnissa. Usein momentum tuottaa paperilla isoja tuottoja, mutta on kulujen vuoksi vaikeampi saada tuottamaan oikeaa rahaa. Rebalansoinnissa on kuitenkin mahdollista hyödyntää momentumia (joka mahdollisesti nostaa salkun tuottopotentiaalia) ja samaan aikaan pienentää salkun kiertonopeutta (eli kuluja). Momentumin annetaan toimia salkkua rebalansoitaessa myymällä positiivisen momentumin assetteja ja ostamalla negatiivisen momenttumin assetteja viivästetysti eli antamalla target-painojen ylittyä ja alittua. 

Yksi tapa on myös säätää assettien target-painoja valuaatioiden perusteella. Ehkä en lähtisi tekemään sitä niinkään yksittäisten osakkeiden kesken, mutta esimerkiksi ETF-tasolla säätämällä hiljalleen assetin target-painoa esim. Shillerin P/E:n perusteella. Tässä yhdistettäisiin tavallaan value-tyyli rebalansointiin painottamalla halvoilta vaikuttavia assetteja enemmän. Tässä suosisin pieniä taktisia valuaatioperustaisia muutoksia selkeän alla olevan strategisen allokaation päällä, ettei tulisi tehtyä samaa virhettä minkä itse tein joskus 2015 kun ”rebalansoin” USA-ETFn kokonaan pois salkusta, koska se oli niin ”kallista”. Hajautuksen ja rebalansoinnin yksi idea kun olisi päästä hyötymään niistä korkealle arvostetuista ja jopa kuplaan asti yltävistä asseteista myymällä niitä hitaasti huipulle noustessa ja taas ostaen hiljalleen takaisin matkalla alas. Jos tekee tuollaisen virheen kuin itse tein USA-markkinan kanssa niin jää tämä ilo kokematta.

Lisäksi tuollainen equally weighted portfolio on käytännössä osittain paperituottoja, koska se korostaa microcappeja jotka ovat epälikvidejä ja joiden rebalansointi jo spredeistä johtuen olisi hyvinkin kallista. Itse tykkään esimerkiksi Research Affiliates -firman RAFI indeksistä, joka painottaa assetteja fundamenttien perusteella (esim. book value, osinkotuotto, sales jne.) markkina-arvon sijaan. Tällä tavalla painot muuttuvat hitaasti firman ”fundamentaalisen painon mukaan” ja lisäksi epälikvideimmät firmat tiputetaan indeksistä, jolloin saadaan rebansointi hoidettua järkevillä kuluilla. Käytännnössä nämä ovat value-ETFiä, joita olen aikoinaan ostanut salkkuuni. Nykyäänhän parhaan ETF-teknologian (eli USAn ETFien) ostaminen onkin kielletty meiltä Eurooppalaisilta…

Equally weighted on siitä mielenkiintoinen painotus, että se antaa sivutuotteena smallcap value altistuksen ja negatiivisen altistuksen momentum-faktorille. Rebalansointiprosessissa kun myydään nousseita ja ostetaan laskeneita (value, negatiivinen momentum) ja lukumääräisesti pieniä firmoja on paljon enemmän (size). Tämä on yksi syy miksi naiivi equally weighted painotus on ollut vaikea voittaa historiassa (historissa smallcap value on tuottanut hyvin). Toinen syy on, että equally weighted lähtökohtaisesti maksimoi hajautuksen ja näin minimoi volatiliteetin (jos oletetaan että kaikki osakkeet/assetit omaavat saman tuottojakauman, mikä ei ole oikeasti täysin realistinen oletus), jolloin geometrisen tuoton ”volatility drag” minimoituu. 

Juha X kirjoitti:

Jonkinlaisena ”reality-checkinä” katsoin, miten yksittäiset osakkeet (pörssi ja First North) ovat pärjänneet Seligsonin OMXH25-etf:lle 10 viime vuoden aikana.

Tämähän oli mielenkiintoinen katsaus Suomen markkinaan. Eli vaikkei vertailu ole ihan yksi yhteen minun USAn markkina-tutkimuksen kanssa, niin isossa kuvassa näyttää hyvin samankaltaiselta nuo sinun tulokset. Esimerkiksi tuo minun log-normal malli sanoo USAn markkinan parametreilla, että 20% yhden osakkeen portfolioista voittaa markkinatuoton 10 vuoden periodilla. Tuossa Suomi-katsauksessa vastaava luku oli noin 16%. Log-normal malli ennustaa että 1/105 (eli hieman alle prosentti) parhaiten tuottaneista firmoista tuottaisi noin 13 kertaa markkinatuoton. Revenio taisi tuossa tarkastelussa yltää noin 18 kertaiseen tuottoon.

Monesti kuulee sanottavan, että lyhyen aikavälin heilunta (volatiliteetti) ei ole todellinen riski, pääoman pysyvä menettäminen on. Geometrisia tuottoja tarkastellessa kuitenkin volatiliteetti johtaa odotusarvoisesti pääoman (osan pääomasta) pysyvään menettämiseen eli lyhyen aikavälin heilunta johtaa pääoman menettämiseen pitkällä aikavälillä.

Juha X kirjoitti:

Luin aikoinaan Luenbergerin Investment Science -opuksen (1998) loppukappaleista noista Kelly-kriteerin mukaisista sijoituksista diskreeteissä monen periodin todennäköisyyspeleissä ja jatkuvissa osakesijoituksissa sekä portfolion log-optimaalisesta (tehokkaasta) rintamasta. Perusteos päättyi tuohon kiinnostavimpaan aiheeseen. Jäin odottamaan kirjan jatko-osaa, mutta sitä ei tullut.

Minäkin olen tuota kirjaa selaillut, mutta eniten olen tykännyt lukea Ed Thorpelta Kelly-kriteeriin liittyviä julkaisuja. 

Juha X kirjoitti:

Tuosta rebalanssoinnista kysyisin vielä. Palautetaanko noissa tutkimuksissa salkku aina alkuperäiseen N osakkeeseen, niin että samat osakkeet tulevat taas equally-weighted osuuteensa salkuissa (esim. 10 osakkeen salkussa rebalanssoinnin jälkeen kaikki ovat taas 10% painossa, riippumatta siitä, miten ne kuukauden aikana olivat nousseet tai laskeneet)?

Joo, rebalansoin kaikissa empiirisen datan testeissä kuukausittain osakkeet takaisin equally-weighted osuuteensa. Kelly-kriteeri ja siihen perustuvat kaavat olettavat jatkuvan eli äärettömän tiheän rebalansoinnin, mutta käytännössä kuukausittaisella (ja muiden tutkimusten mukaan myös vuosittaisella) päästään lähelle samaa tulosta. Sen huomasin kuitenkin tuossa empiirisessä osuudessa, että kun otetaan isommin vipua (1.5 ja enemmän), niin kuukausittainen rebalansointitaajuus ei enää meinaa riittää. Tämä johtuu osaltaan siitä, että empiiriset tuotot ovat paksuhäntäisiä eli voivat liikkua nopeasti isompia hyppyjä. Eli vivuttaminen vaatii tieheämpää rebalansointia, mikä kuulostaa intuitiivisesti oikean suuntaiselta.

Juha X kirjoitti:

Ja jatkoa: Miten tulokset muuttuisivat, jos ”rebalanssoinnit” tehtäisiin toisin? Jos esimerkiksi yhden osakkeen salkkuun poimittaisiin kuukauden (tai periodin P) voittaja/häviäjä/mediaani, 10 osakkeen salkkuun voittajat/häviäjät/mediaaniympäristö (ts. momenttityyli ja kontraus), jne.?

Jos ymmärrän tämän sinun kysymyksen oikein, niin ehkä tarkoitat, että miten erilaiset sijoitustyylit vaikuttavat. Näitä eri sijoitustyylejä testasin paljonkin empiirisessä osuudessa. Tuossa alkuperäisessä postauksessa minulla oli yksi kuva eri tyylien ”Diversification Premiumista ” (DP), joka kertoo kuinka paljon suurempi geometrinen keskituotto kyseisen tyylin täysin hajautetulla portfoliolla on verrattuna yhden osakkeen portfolioon. Jos ajatellaan eri tyylejä ajan funktiona, niin mitä suurempi DP metriikka, niin sitä suurempi hajonta ajan myötä syntyy eli sitä enemmän hävitään myös korkoa korolle ilmiön tuottamassa varallisuudessa kun hajautus on heikko. Eli kaikkein eniten hajautusta eri tyyleistä vaatisi joku näiden tyylien yhdistelmä: microcap, growth, low ROE, low momentum.

En edellisessä postauksessa huomannut sanoa, että kuvat eivät olleet (toisin kuin ensimmäisessä postauksessa) empiirisestä datasta vaan log-normal mallilla empiiristä parametreista luotuja. Kuvien tarkoitus oli havainnollistaa miten log-normal jakaumat kuvaavat varallisuuden kasvua ajan yli.

Usein kuulee sanottavan, että empiiriset tuotot ovat paksuhäntäisiä eikä niitä voi mallintaa ei-paksuhäntäisillä malleilla (kuten log-normal). Testasin tätä, ja isossa kuvassa log-normal malli kuvaa varallisuuden kasvua erittäin hyvin. Paksut hännät tarkoittaa, että empiirisessä datassa tulokset ovat vielä hieman radikaalimpia, mutta ei kovin paljoa. Paksujen häntien takia hajauttaminen on edelleen vielä hieman tärkeämpää kuin esim. Log-normal malli antaa ymmärtää.

Tuossa alla on kuva, jossa ylempi kuva mallintaa equally-weitghted markkinaportfolion jakauman log-normal mallilla 45.5 vuoden periodilla (käyttäen empiirisen Jan/1973 – Jun/2018 periodin parametreja). Otan yhden pisteen (punainen pallo) eli tuolla periodilla realisoituneen markkinatuoton ja siitä ikään kuin zoomataan alempaan kuvaan, jossa näytetään eri kokoisten portfolioiden tuottamat varallisuudet prosentuaalisessa suhteessa markkinan tuottaman varallisuuteen. Vasemmalla olevat numerot ovat log-normal mallin tuottamia ja oikealla puolella empiirisestä datasta simuloidut arvot. Numerot ovat hyvin lähellä toisiaan. Ainoa poikkeus on, että empiirisestä (paksuhäntäisestä) datasta simuloidut mediaanivarallisuudet ovat jonkin verran heikompia suhteessa markkinaan kuin log-normal malli antaa ymmärtää. Esimerkiksi 10 osakkeen portfolio häviää log-normaalissa mallissa 49% markkinalle, kun se empiirisessä datassa häviää 53%. Todennäköisyydet ovat hyvin lähellä toisiaan. Esimerkiksi todennäköisyys että 10 osakkeen portfolion varallisuus on kaksi kertaa suurempi kuin markkinaportfolion tuottama varallisuus on log-normaalissa mallissa 11.9% ja empiirisessä datassa 11.7%.

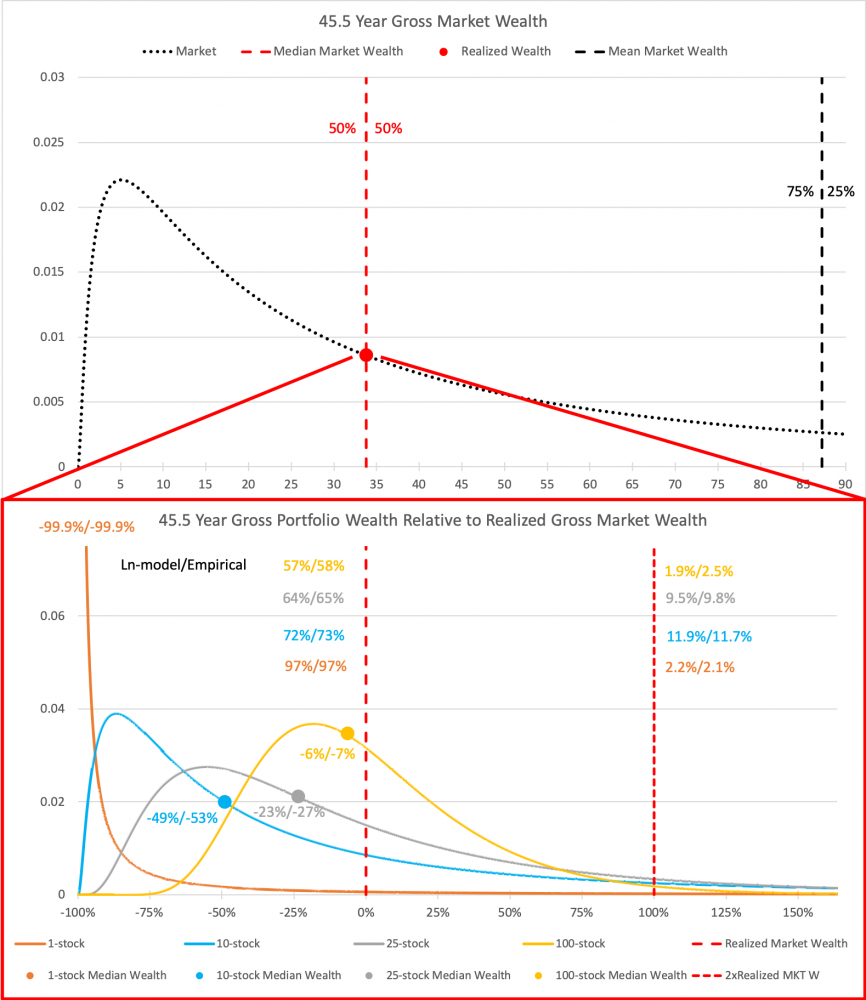
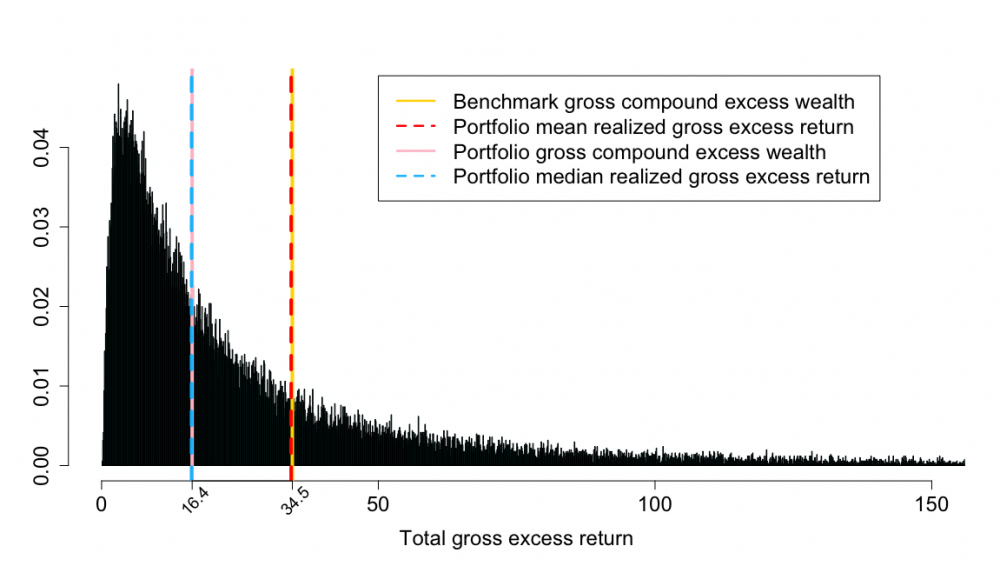
Tässä alla vielä vertailun vuoksi empiirisestä datasta ajettu jakauma 10 osakkeen portfoliolle.

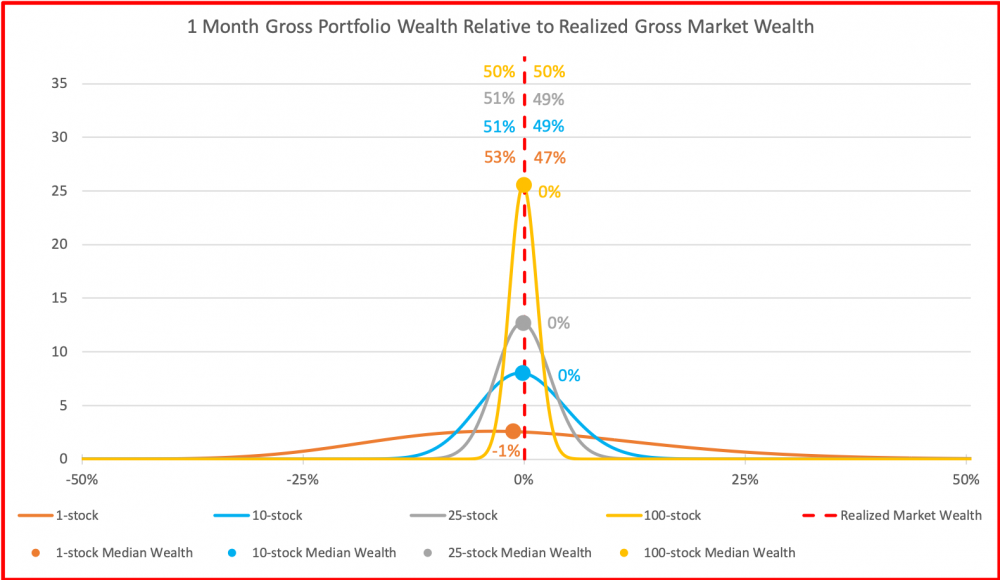
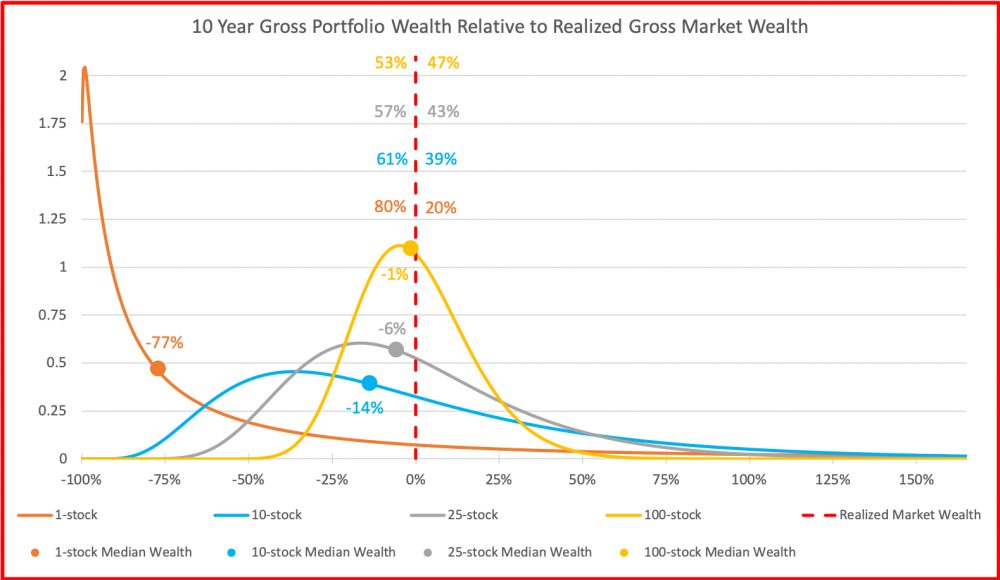
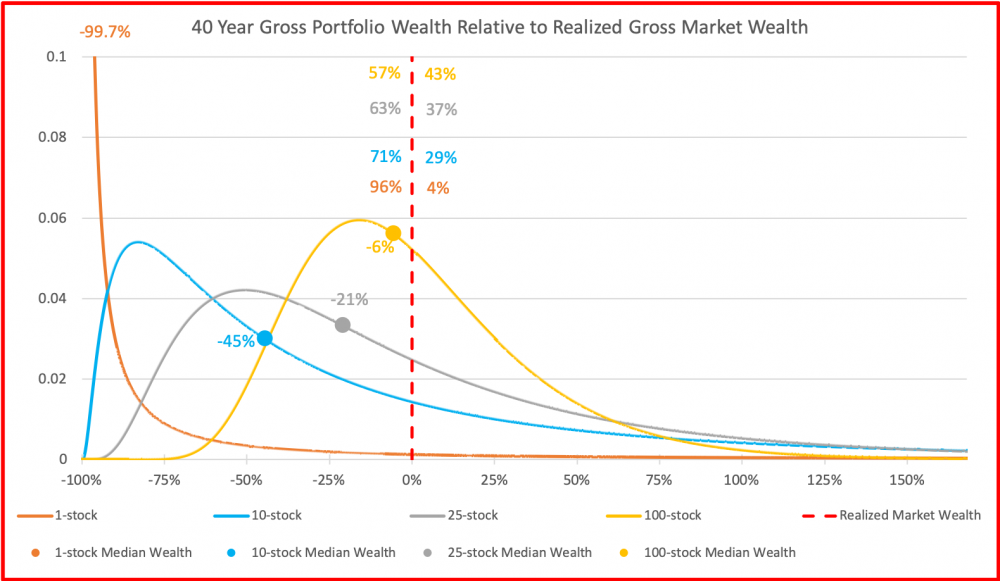
Tässä vielä sarja log-normal mallilla ajettuja kuvia, joissa näkyy eri portfoliokokojen varallisuuden suhteellinen vertailu markkinaportfolion tuottamaan varallisuuteen eri periodeilla:  

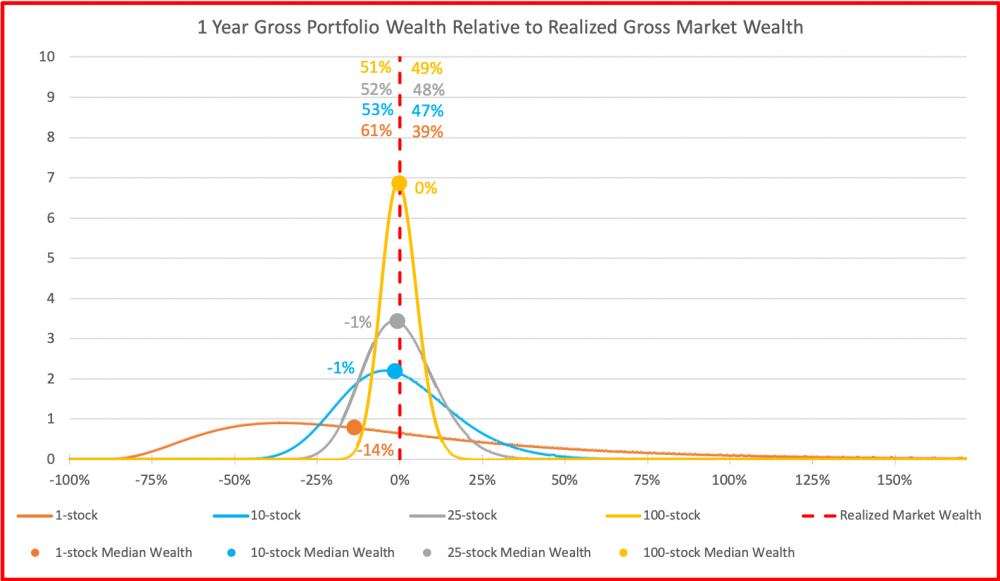
Ja tässä vielä vauvasta eläkkeelle kuva. Joku vuosi sitten oli julkisuudessa kovasti keskustelua ”lapsilisillä miljonääriksi” -teemasta. Tämä näkökulma jäi silloin käymättä läpi: Jos hajautus ei ole kunnossa, niin suurimmasta osasta lapsia ei tule miljonäärejä, vaikka markkinaportfolio tuottaisi miljoonan. Osasta lapsia tosin tulee monimiljonäärejä.

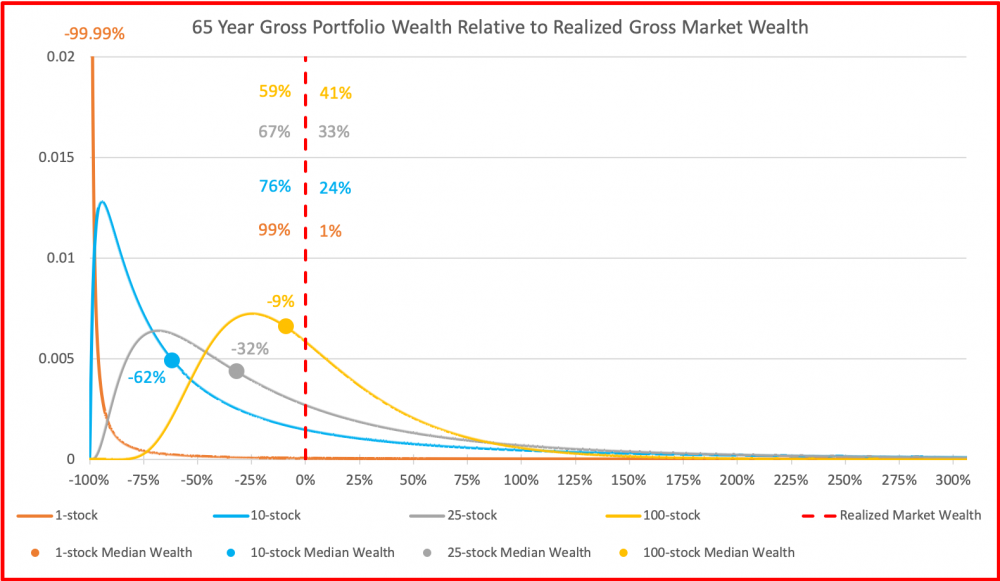
Kuvista nähdään, että kun sijoitushorisontti pitenee niin mediaanitappiot markkinaportfolion tuottamalle varallisuudelle kasvavat. Samoin entistä suurempi prosentti portfolioista häviää markkinalle. Vastapainona oikeassa hännässä varallisuudet kasvavat entisestään. 

Oleellinen pointti tässä on, että mikäli halutaan pitää odotettu mediaanivarallisuus esim. 90% tasolla markkinan tuottamaan varallisuuteen, niin hajautuksen täytyy kasvaa samaa tahtia kuin aika kasvaa. Jos 10 vuoden periodilla 10 osaketta oli riittävä hajautus, niin 20 vuoden periodilla tarvitaan 20 osaketta ja 40 vuoden periodilla 40.

Näin tarkasteltuna hajauttaminen on sitä tärkeämpää mitä pidempi sijoitushorisontti. Eli täsmälleen päinvastoin kuin yleensä ajatellaan.

madgecko kirjoitti:

Tarkoittaako tämä käytännössä jotain? Eikö kaikki pyri hyötymään korkoakorolle ilmiöstä?

Korkoa korolle ilmiö vaatii aikaa, jotta sen vaikutukset alkavat kunnolla näkyä. Osakesijoittajille muistutetaan aina pitkän sijoitushorisontin tärkeydestä. Markowitzin malli, joka perustuu aritmeettisiin tuottoihin ja opetetaan kaikissa alan kouluissa, on staattinen yhden periodin malli. Käytännössä tämä tarkoittaa, että malli jo rakenteensa puolesta ei huomio aikaa mitenkään. Geometriset tuotot puolestaan kuvaavat tuottoa ajan yli. Geometrisessa mallissa tuotot sijoitetaan aina edelliseltä periodilta seuraavalle, jolloin korkoa korolle -ilmiö pääsee toimimaan.

Ja kyllä, suurin osa osakesijoittajista haluaa hyötyä nimenomaan korkoa korolle -ilmiöstä ajan yli. Eli pointti on, että Markowitzin malli ei ole paras mahdollinen todellisen sijoittajan tarpeisiin, koska todellinen sijoittaja elää maailmassa, jossa on aika (ja jossa sijoittajat mittaavat sijoitustuottojaan geometrisina tuottoina). 

madgecko kirjoitti:

Entä jos salkussa on osakepaino 50% tai 150% (eli +50% velkaa) niin miten hajauttaminen eroaa käytännössä näissä tilanteissa?

Hajauttamisen vaikutus geometrisiin tuottoihin eri osakepainoilla näkyy alkuperäisen postauksen ensimmäisessä kuvassa. Jos verrataan 50% osakepainon kohdalla vaikka 10 osakkeen portfoliota täysin hajautettuun benchmarkiin (BM), niin ero on pieni, ehkä vajaa 0.5 prosenttiyksikköä. Kun katsotaan eroa 150% osakepainon kohdalla, niin ero on paljon suurempi, noin 3.5 prosenttiyksikköä. Eli suurella osakepainolla hajautushyöty on tuotto-odotuksella mitattuna paljon suurempi eli hajauttaminen on sitä tärkeämpää mitä suurempi osakepaino on.

Eli geometrisia tuottoja käytettäessä tuotto-odotus kasvaa, mutta koko ajan hitaammin (kääntyen lopulta pieneneväksi ja negatiiviseksi johtaen lopulta kaiken varallisuuden menettämiseen) kun osakepainoa lisätään. Samalla riski (volatiliteetti) kasvaa lineaarisesti eli riskikorjattu tuotto laskee jatkuvasti osakepainon noustessa. Markowitzin mallissa aritmeettinen tuotto-odotus kasvaa lineaarisesti kohti ääretöntä osakepainon noustessa kohti ääretöntä. Riskikorjattu tuotto (Sharpe ratio) pysyy vakiona. Eli Markowitzin malli ei näe muuta riskiä osakepainon lisäämisessä kuin kasvaneen volatiliteetin kun geometrisiin tuottoihin perustuva malli näkee sekä tuotto-odotuksen pienenemisen (ja lopulta kääntymisen negatiiviseksi) ja kasvaneen volatiliteetin. Äärettömällä vivulla Markowitzin malli johtaa odotusarvoisesti äärettömään varallisuuteen, kun geometrinen malli johtaa lähes varmaan varallisuuden täydelliseen menettämiseen.

Käytännössä geometrinen keskituotto vastaa mediaanituottoa eli tyypillistä varallisuuden kasvua. Aritmeettinen keskituotto puolestaan on kaikkien mahdollisten tuottojen yksinkertainen keskiarvo, joka varsinkin heikolla hajautuksella ja/tai pitkällä aikavälillä usein kuvaa todella huonosti tyypillistä varallisuuden kehitystä. 

Alla neljä kuvaa varallisuuden kehityksestä eri mittaisilla periodeilla. Ensimmäinen kuva on kuukauden periodilla, jolloin Markowitzin malli kuvaa vielä varallisuuden kehitystä hyvin. Kaikki käyrät ovat suunnilleen normaalijakautuneita ja hajautuksen vaikutus näkyy niin, että paremmin hajautettujen portfolioiden jakaumat ovat kapeampia. Kaikkien portfoliokokojen mediaanit ovat samat kuin markkinaportfolion tuotto (paitsi 1 osakkeen portfoliolla -1% markkinaportfoliosta).

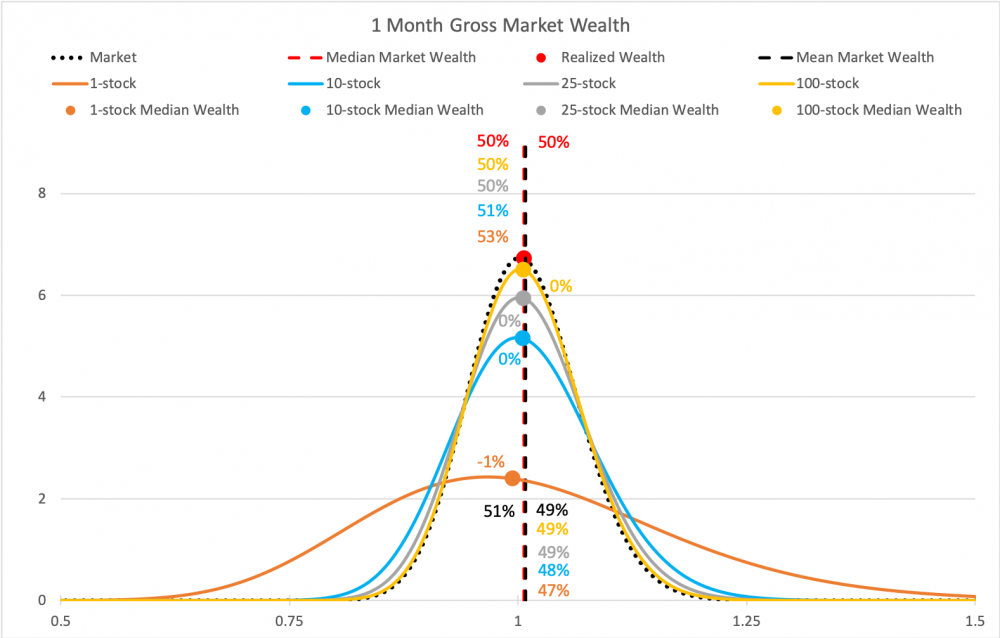
Toinen kuva on vuoden periodilta. Nyt alamme nähdä pieniä eroja. 1 osakkeen portfolion mediaani on jo jäänyt 14% alle markkinatuoton ja 60% 1 osakkeen portfoliosta jää alle markkinatuoton. Musta katkoviiva (markkinan tuottaman varallisuuden aritmeettinen keskiarvo) on hitusen irronnut punaisesta katkoviivasta (markkinan tuottaman varallisuuden mediaani). 

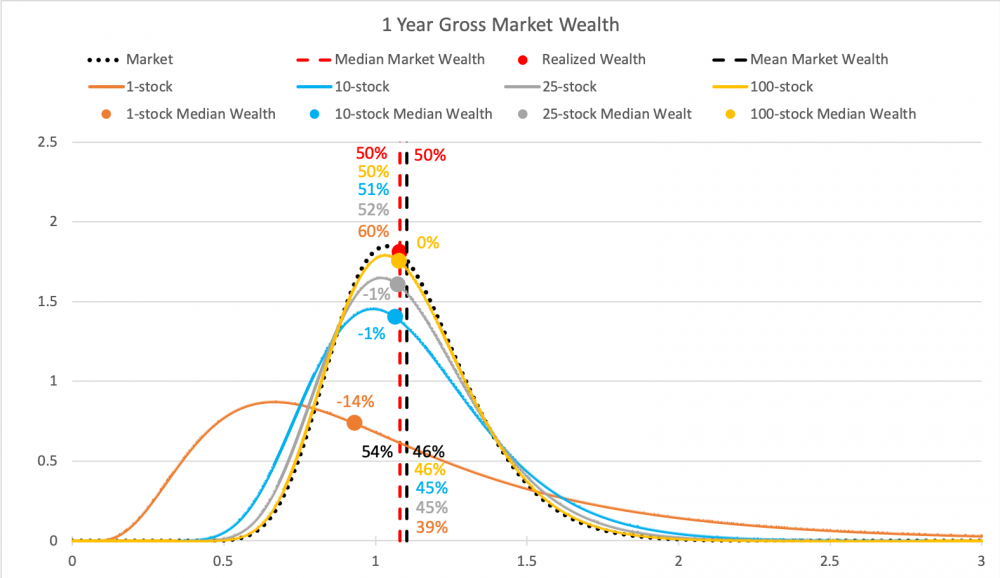
Kolmas kuva on 10 vuoden periodilta. Nyt aika jo tehnyt tehtävänsä ja Markowitzin malli ei enää kuvaa ollenkaan tyypillistä 1 osakkeen portfoliolla sijoittavan varallisuutta. Mediaanivarallisuus kyseisellä sijoittajalla on -77% verrattuna markkinan tuottoon ja jakaumat eivät enää muistuta normaalijakaumaa vaan log-normaalia jakaumaa. 

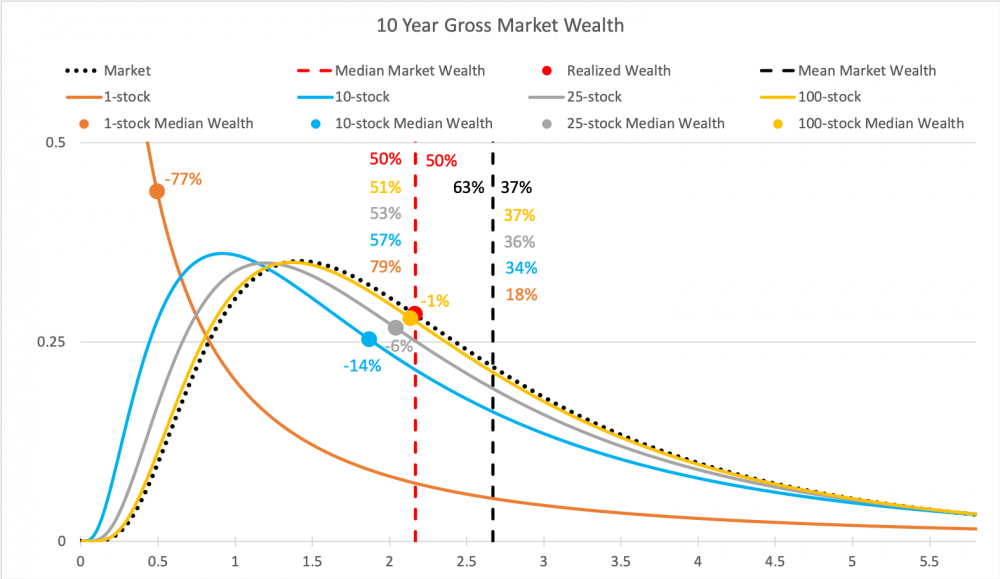
Neljäs kuva on eläkesijoittajan 40 vuoden periodilta. Nyt 1 osakkeen portfoliolla on tyypillisesti hävitty käytännössä kaikki (ja ollaan -99.7% verrattuna markkinan tuottamaan varallisuuteen). Myös 10 osakkeen portfoliolla on tyypillisesti hävitty markkinalle 45%, 25 osakkeella 21% ja 100 osakkeellakin 6%. Vastapainona jakauman oikeassa hännässä (kaukana kuvan ulkopuolella) on Bill Gates, joka on sijoittanut vuosikymmeniä yhteen menestyneeseen osakkeeseen ja jonka varallisuus (muutaman muun supermenestyjän avittamana) riittää nostamaan 1 osakkeen portfolioiden keskiarvon markkinatuoton tasolle.

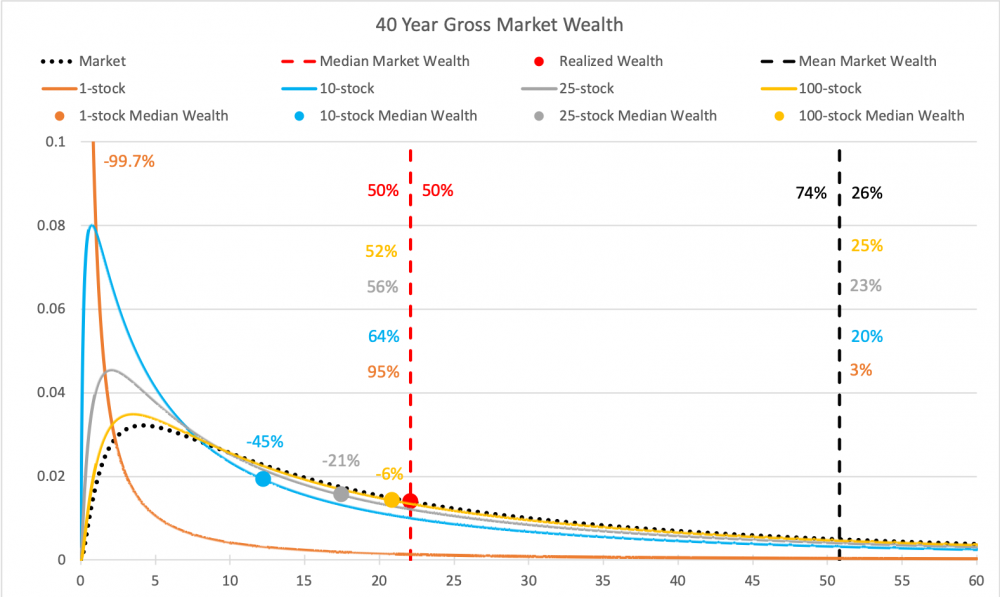
Eli katsottuna pitkän ajan yli kertyneitä varallisuuksia, geometriset tuotot (jotka kuvaavat mediaania eli tyypillistä kehitystä) ovat paljon kuvaavampia yksilön kannalta kuin Markowitzin malli, joka ei näe eroa tuotto-odotuksessa 1-osakkeen portfoliolla ja markkinaportfoliolla sijoittavien välillä.

Ajattelin lisätä tähän ketjuun kvantitatiivisen analyysin PYN Elitestä. Olen itse sijoittanut PYN Eliteen nyt reilun viiden vuoden ajan. Enimmäkseen käytän indeksituotteita, mutta PYN Eliten kohdalla olen tehnyt poikkeuksen. 

Tämä analyysi ei niinkään keskity analysoimaan PYN Eliteä erillisenä rahastona, vaan portfolion komponenttina. Analysoin siis PYN Eliteä assettina, en portfoliona.

Portfoliolle tärkeinä parametreina pidän Sharpen lukua ja geometrista tuotto-odotusta. Assetille sen sijaan tärkeää on sen aritmeettinen tuotto-odotus ja korrelaatio muiden portfolion assettien kanssa.

Jaoin PYN Eliten historian karkeasti ensin kahteen periodiin: 1) Thaimaa 02/1999 --> 05/2013 ja 2) Thaimaan jälkeinen aika 06/2013 --> 11/2020. Thaimaan jälkeisellä periodilla rahasto oli sijoitettuna myös Kiinan markkinoilla ja siirtyi täysin Vietnam-painoon noin keväällä 2017. Muodostin vielä kolmannen periodin: 3) Vietnam 04/2017 --> 11/2020.

Aloitetaan korrelaatioista. Käytän analyysissä kuukausituottoja. Otoskorrelaatiot voivat vaihdella isosti samastakin datasta mitattuna, kun tuottojen ”pituutta” vaihdetaan. Esimerkiksi kuukausituotosta mitattu korrelaatio voi muuttua paljonkin, kun vaihdetaan kahden kuukauden mittaisiin tuottoihin. Siksi mittasin korrelaatiot, yhden, kahden, kolmen ja neljän kuukauden tuotoille ja laskin näille keskiarvon. Tämä antaa paremman kuvan korrelaatioista etenkin epälikvideille assetteille (jollainen PYN Elite näyttää olevan tulevan analyysinkin perusteella), jotka liikkuvat ”hitaammin”.

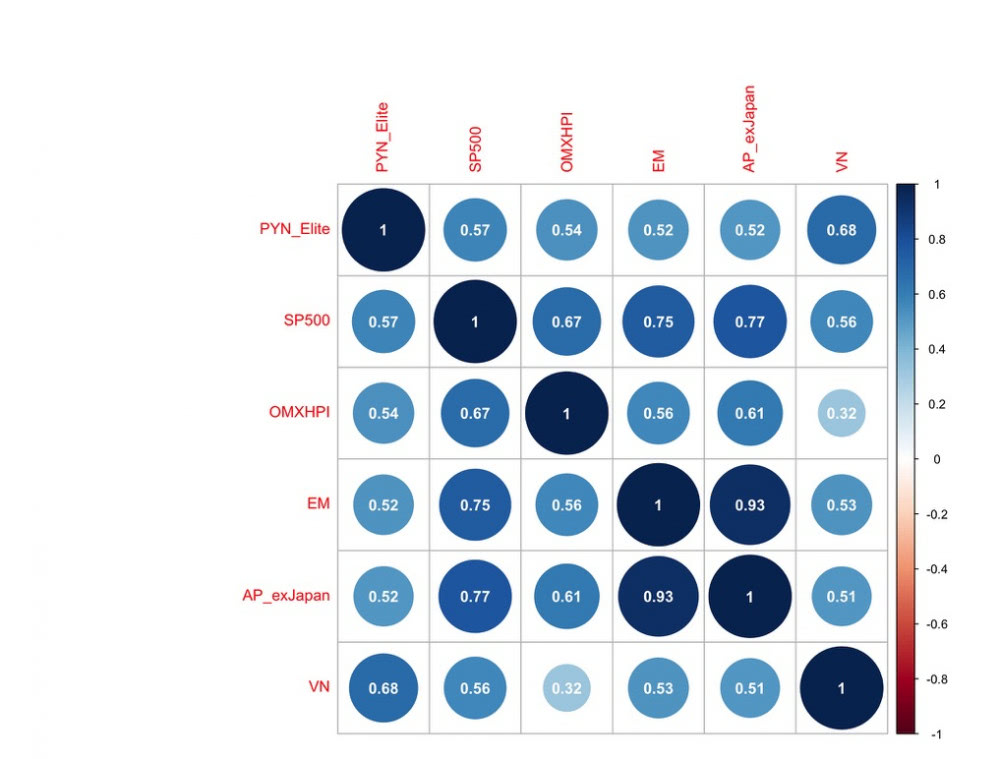
Alla olevassa kuvassa nähdään PYN Eliten korrelaatiot merkittäviin indekseihin Thaimaa-periodilla. Ilahduttavasti suomalaisen sijoittajan kannalta sekä PYN Eliten, että Thaimaan markkinan (SET) korrelaatio OMXHPI indeksiin on ollut pieni. PYN Eliten korrelaatio kaikkiin merkittäviin indekseihin (lukuun ottamatta SET indeksiä) on maltillinen eli rahasto on tuonut merkittävää hajautushyötyä. Korrelaatio-matriisista nähdään myös, että Asia Pacific excluding Japan indeksi korreloi todella vahvasti kehittyvien markkinoiden (EM) kanssa. EM-indeksi voisi tämän perusteella toimia myös PYN Eliten vertailuindeksinä APExJapan indeksin sijaan.

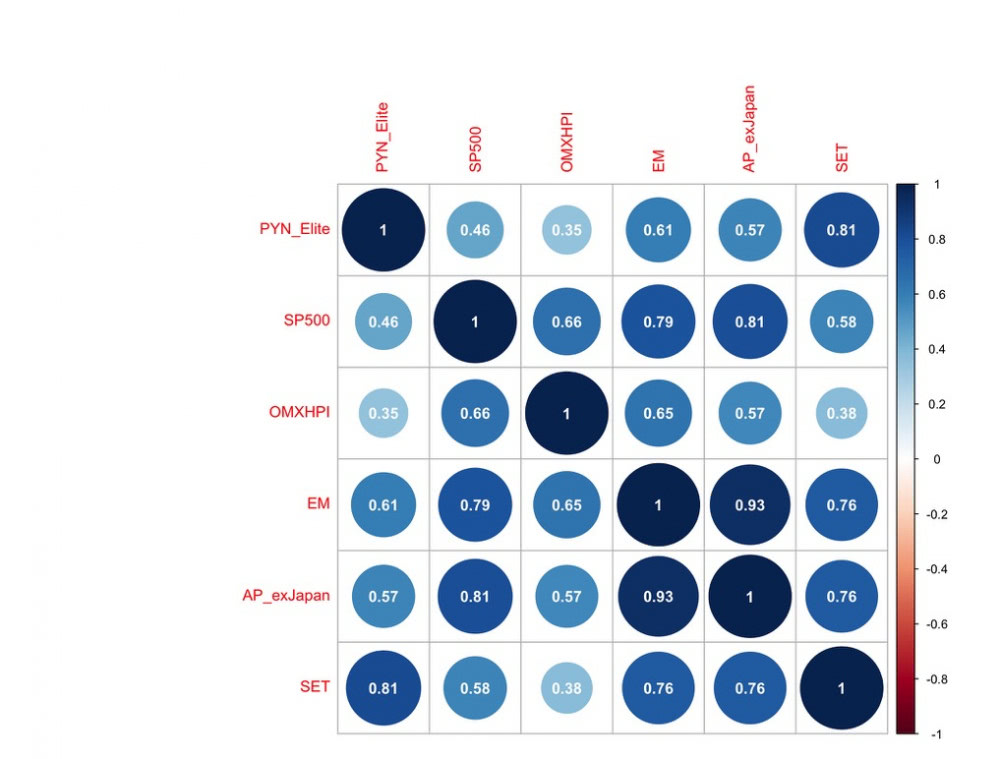
Seuraavassa kuvassa nähdään korrelaatio Thaimaan jälkeisellä (06/2013 -->) periodilla. Verrattuna Thaimaa-periodiin, PYN Eliten korrelaatio Suomen markkinaan on hieman noussut, mutta yleisesti ottaen korrelaatiot ovat edelleen maltillisia. Hajautushyötyä on siis tullut myös viime aikoina. Erityisen ilahduttavaa on, että Vietnamin markkinan (VN indeksi) korrelaatio OMXHPI indeksiin on hyvin pieni. 

Seuraavaksi yritän selittää PYN Eliten tuotot ja riskit faktorimallien avulla. Lähtökohtaisesti oletan, että suurin osa rahaston tuotoista ja riskistä selittyy kohdemarkkinan tuotoilla ja riskeillä. Siksi valitsen faktorimalliin Thaimaa-periodille SET-indeksin excess tuoton (SET_eret) eli indeksin ylituoton riskittämään korkoon nähden (RF). Riskittömänä korkona käytän tässä helppouden vuoksi USAn kuukausittaista treasury-korkoa. Käyn läpi myös kaikki Fama-French 5-factor mallin faktorit ja momentum-faktorin kun etsin mallia, joka kuvaa rahaston tuottoja ja riskiä. Käyn läpi nämä faktorit Asia Pacific excluding Japan sekä emerging markets alueille. EM-faktorit näyttävät kuvaavan tuottoja hieman paremmin. Lisäksi otan faktoriksi EUR/USD kurssin tuottohistorian. 

Normaalien faktoreiden lisäksi käytän regressiossa viivästettyjä faktoreita. Käytän ns. Dimson-Betaa eli viivästetyä faktoria, joka paljastaa rahaston mahdollisen viiveellä tapahtuvan reagoinnin faktoriin. 

Alla näkyy paras malli minkä löysin kuvaamaan Thaimaa-periodia. Kaikki mallin faktorit ovat tilastollisesti merkittäviä. Myös alpha (eli selittämätön tuotto, tai Deryngin osakepoimintataito) on tilastollisesti merkittävä. Malli selittää noin 67% PYN Eliten tuottojen varianssista. Merkittävä osa riskistä, 33%, jää selittämättömäksi. Regressio myös näyttää, että sekä Thaimaan indeksi että size factor selittävät PYN Eliten tuottoja myös viivellä (lag1_ -faktorit). Laskemalla yhteen normaalit ja viivästetyt faktorit (esim. SET_eret+lag1_SET_eret) nähdään faktorin todellinen vaikutus rahaston tuottoihin. Lagged-faktorit vihjaavat, että PYN Eliten tuotot ovat syntyneet hyvin epälikvideistä sijoituksista. Mallin mukaan tuotto on syntynyt rahaston altistuksesta SET indeksille, EM size faktorille sekä EUR/USD kurssivaihteluille. Lisäksi rahaston tuottoon on vaikuttanut erittäin suuri selittämätön tuotto, alpha (alpha eli intercept kuvassa on kuukausitasolla). 

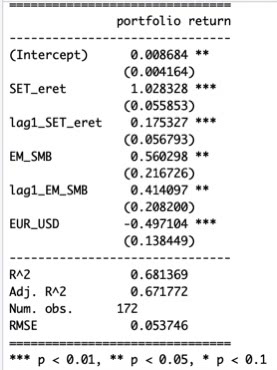
Tässä kohtaa on kuitenkin hyvä huomata, että käytän Thaimaan SET indeksiä, joka on hintaindeksi (ei kokonaistuottoindeksi). SET indeksi ei siis sisällä osinkotuottoa. Näin ollen PYN Eliten osinkotuotto käsittääkseni näkyy regressiomallissa selittämättömänä tuottona eli on osa alphaa. Löysin SET TRI (SET total return indeksin) alkaen 09/2003. Alla näkyvässä kuvassa ajan regression, jossa selitän total return indeksin tuottoja hintaindeksillä. Kuvasta nähdään, että markkinabeta on 1 ja malli selittää käytännössä 100% tuottojen varianssista, mutta alpha on annualisoituna 4.22%. Arvioin tästä, että Thaimaan SET indeksin yhtiöiden osinkotuotto on ollut tuo reilu 4% periodilla 09/2003 --> 05/2013. Jos oletamme saman reilut 4% osinkotuoton koko Thaimaa-periodille ja pidämme sitä myös PYN Eliten ”normaalina osinkotasona”, päädymme noin (0.008684*12 – 4.22) 6% vuosittaiseen alphaan. Myös regression alphan tilastollinen merkittävyys heikkenisi, jos meillä olisi total return indeksi (joka huomioisi osingot) koko periodille hintaindeksin sijaan.

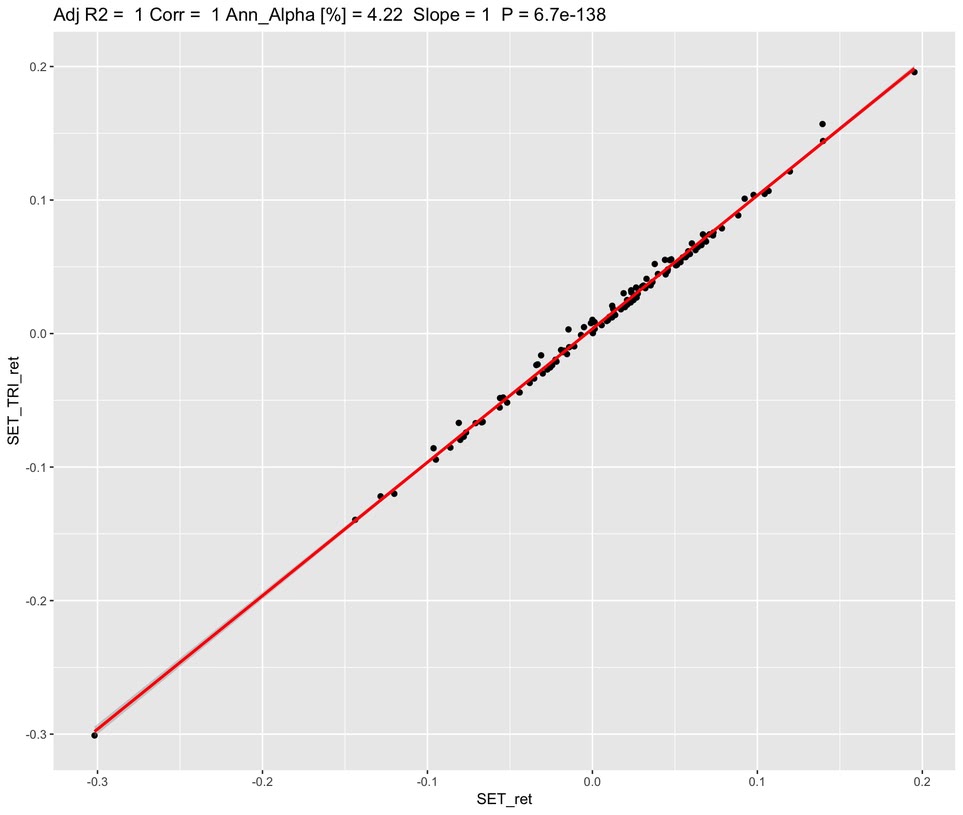
Thaimaa-periodin tuoton voidaan mallin mukaan arvella muodostuneen sijoituksista epälikvideihin pieniin (tai hyvin pieniin microcap?) yhtiöihin, joiden tuotot ovat reagoineet voimaakkaasti Thaimaan osakemarkkinan liikkeisiin. Mahdollisesti Deryng on myös pystynyt hyödyntämään osakepoimintataitoaan isosti epätehokkailla ja epälikvideillä microcap markkinoilla?

Paljonko eri faktorit olisivat sitten tarjonneet tuottoa Thaimaa-periodilla? Tämä näkyy seuraavassa kuvassa.

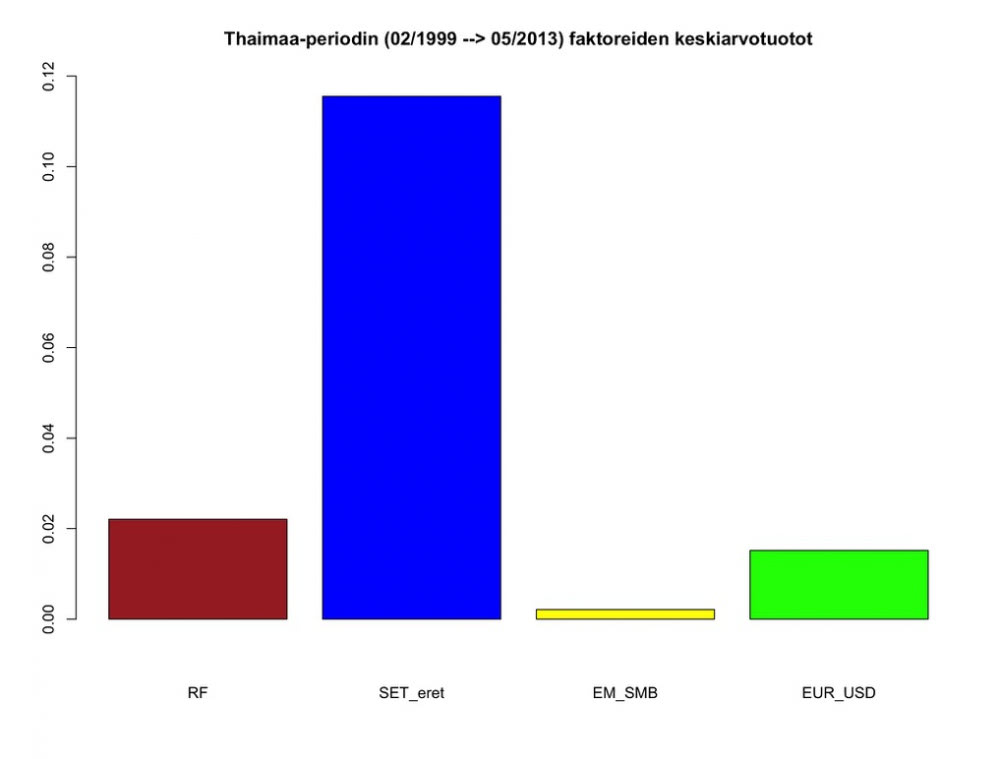
Kuvasta nähdään, että Thaimaan hintaindeksi tuotti lähelle 12% per vuosi (ja osinkoja arviolta se 4% tähän päälle), kun size-faktorin tuotto jäi lähelle nollaa. Euro vahvistui vajaat pari prosenttia per vuosi. 

Kertomalla regressio-analyysistä saaduilla kertoimilla faktoreiden tuotot, saadaan mallin tuottamat PYN-Eliten tuottokomponentit. Seuraavassa kuvassa nähdään PYN-Eliten aritmeettinen tuotto sekä tuoton muodostaneet komponentit.

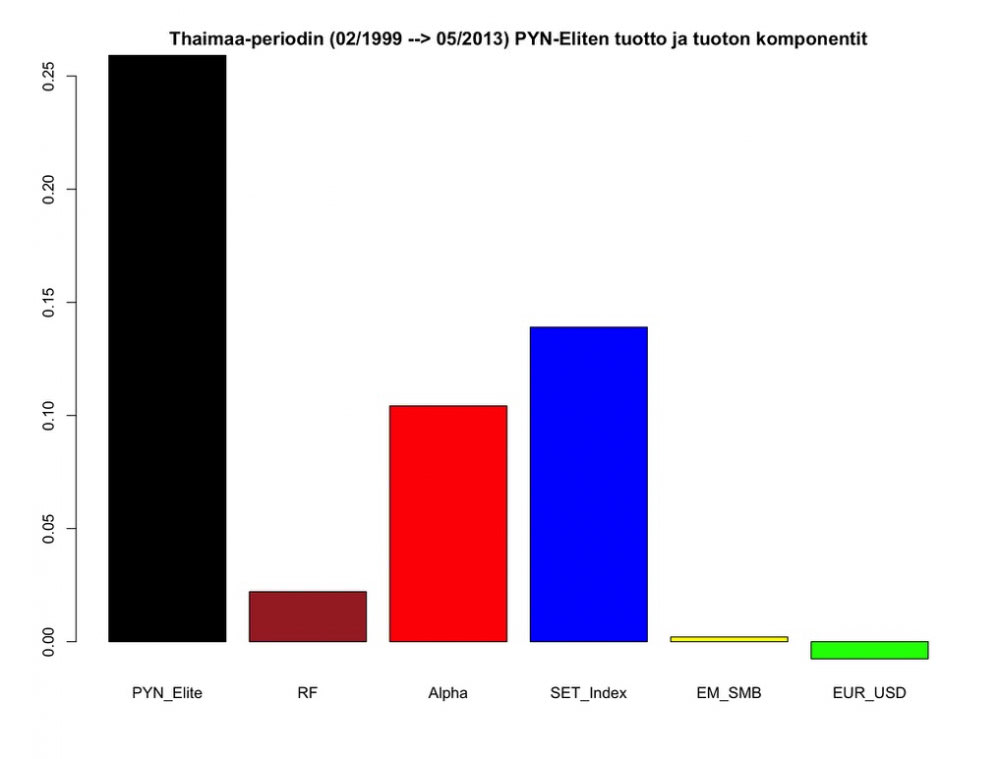
Kuva kertoo, että suurin kontribuutio PYN Eliten tuottoon tuli Thaimaan pörssimarkkinan tuotosta. Seuraavaksi suurin kontribuutio tuli selittämättömästä lähteestä (Alpha), jonka voidaan ajatella olevan osittain korvausta epälikvidiys-riskin kantamisesta (”illiquidity premium”), mutta myös salkunhoitajan taitoa. Kun huomioimme osingot, arviolta 4 prosenttiyksikköä pitäisi kuitenkin siirtää punaisesta alpha-pylväästä siniseen SET index -pylvääseen. Muut komponentit ovat lähes merkityksettömiä. Vaikka rahasto altistui voimakkaasti size-faktorille, ei faktori tuottanut periodilla mitään. Siitä ei siis saatu vetoapua tuottoihin. Valuuttakurssimuutokset periodilla olivat epäsuotuisia (Euro vahvistui), mutta vaikutus rahaston tuottoihin on minimaalinen. Tämä voisi johtua onnistuneesta valuuttasuojauksesta (en ole tarkistanut milloin tarkalleen valuuttasuojauksia oli).

Seuraavaksi periodi Thaimaan jälkeen.

Kuvassa nähdään regressioanalyysin tulos parhaalle mallille minkä löysin. Malli selittää rahaston tuottojen varianssista noin 70%. Mallin mukaan periodin tuotto koostuu tilastollisesti merkittävistä Vietnamin markkinan tuotosta, smallcap value altistuksesta sekä valuttaakurssimuutoksista. Selittämätön tuotto (alpha) ei ole tilastollisesti merkittävä, eikä myöskään kovin suuri. Tällä periodilla viivästetyt betat eivät olleet merkittäviä. Tämä voisi johtua siitä, että rahaston koko on kasvanut alkuajoista merkittävästi, jolloin on siirryttävä pienimmistä microcap yhtiöistä suurempiin small/midcap yhtiöihin, jotka eivät ole yhtä epälikvidejä (eivätkä yhtä epätehokkaasti hinnoiteltuja)?

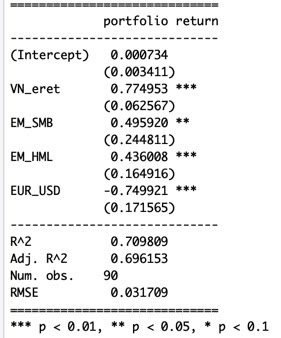
Seuraava kuva näyttää periodin faktoreiden keskituotot. VN hintaindeksi on tuottanut hyvin, mutta small cap altistus on tuonut hieman vastatuulta.

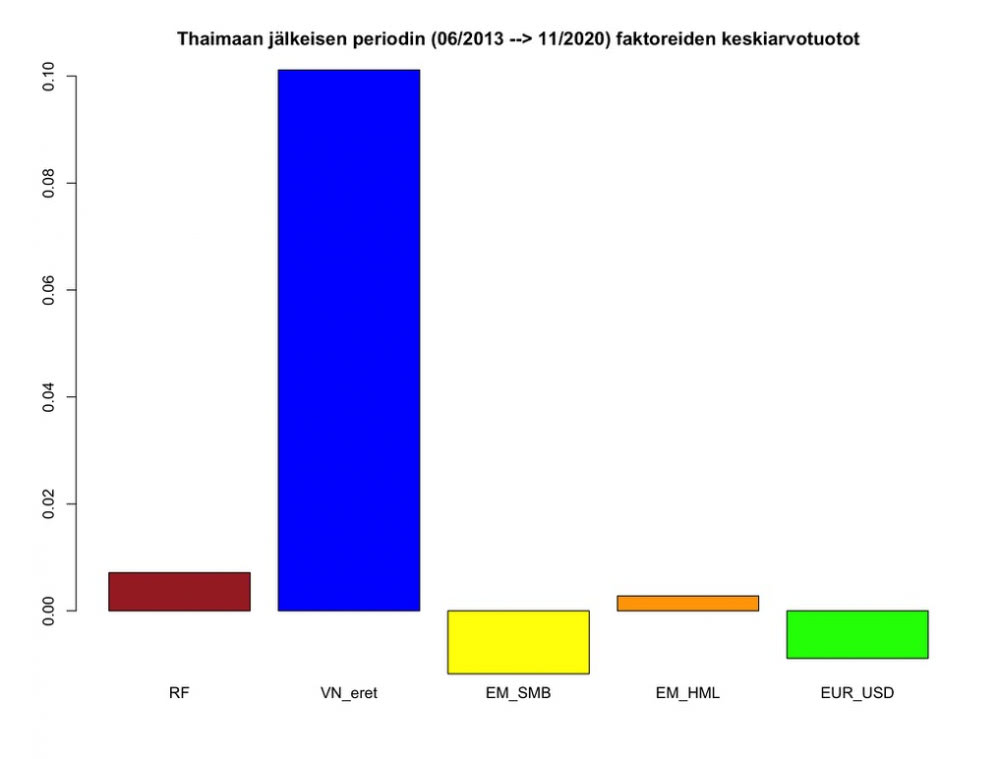Seuraavaksi PYN Eliten tuotto sekä sen komponentit. Altistuminen Vietnamin markkinatuotolle on merkittävin komponentti. Small cap on tuottanut hieman tappiota. Alpha tällä periodilla on pieni (ja oletettavasti negatiivinen, jos huomioimme osingot). Rahaston suurempi koko alkaa vaikuttaa? Valuuttakurssin tuoma pieni myötätuuli on koitunut rahaston eduksi. 

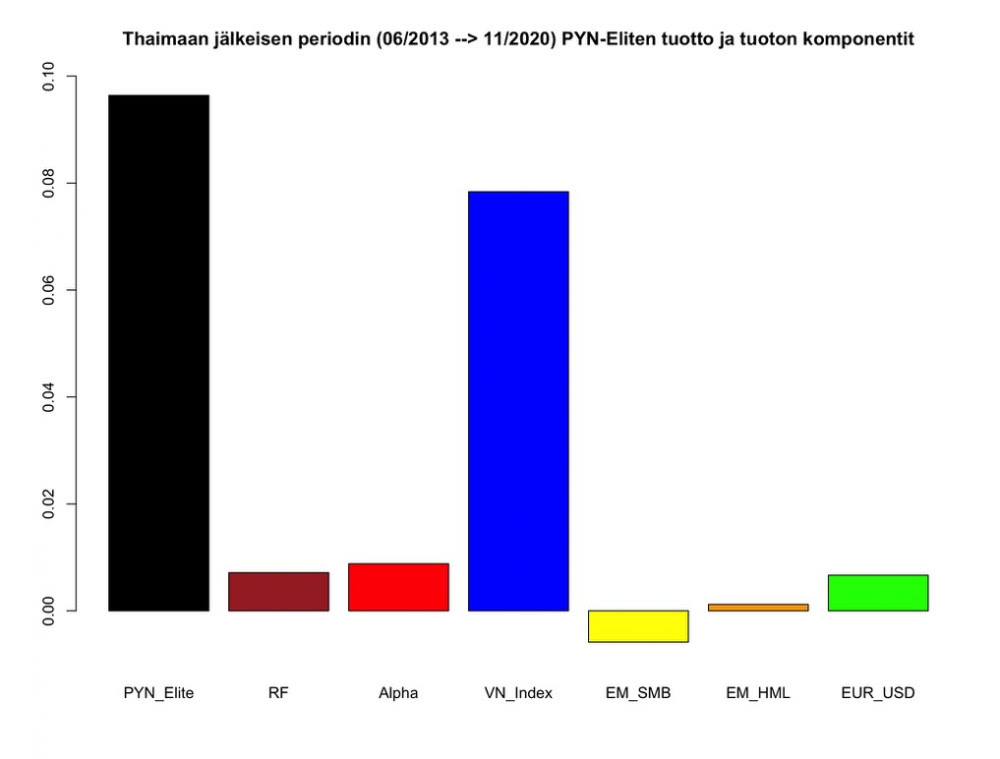Lopuksi katsomme vielä kolmatta periodia, jolloin rahasto on ollut 100% Vietnamissa. Regressioanalyysi näyttää, että periodin tuotto on muodostunut VN indeksistä sekä smallcap value altistuksesta. Nämä ovat tilastollisesti merkittäviä. Valuuttakurssimuutokset ja alpha eivät ole tilastollisesti merkittäviä. Malli selittää rahaston tuottojen varianssista noin 81%.

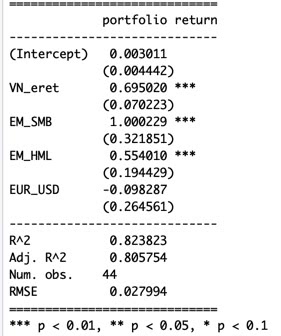
Seuraavassa kuvassa periodin faktoreiden keskiarvotuotot. Kuva kertoo, että smallcap valuella ei ole mennyt hyvin tällä periodilla. Samoin valuuttakurssi on kehittynyt epäedullisesti.

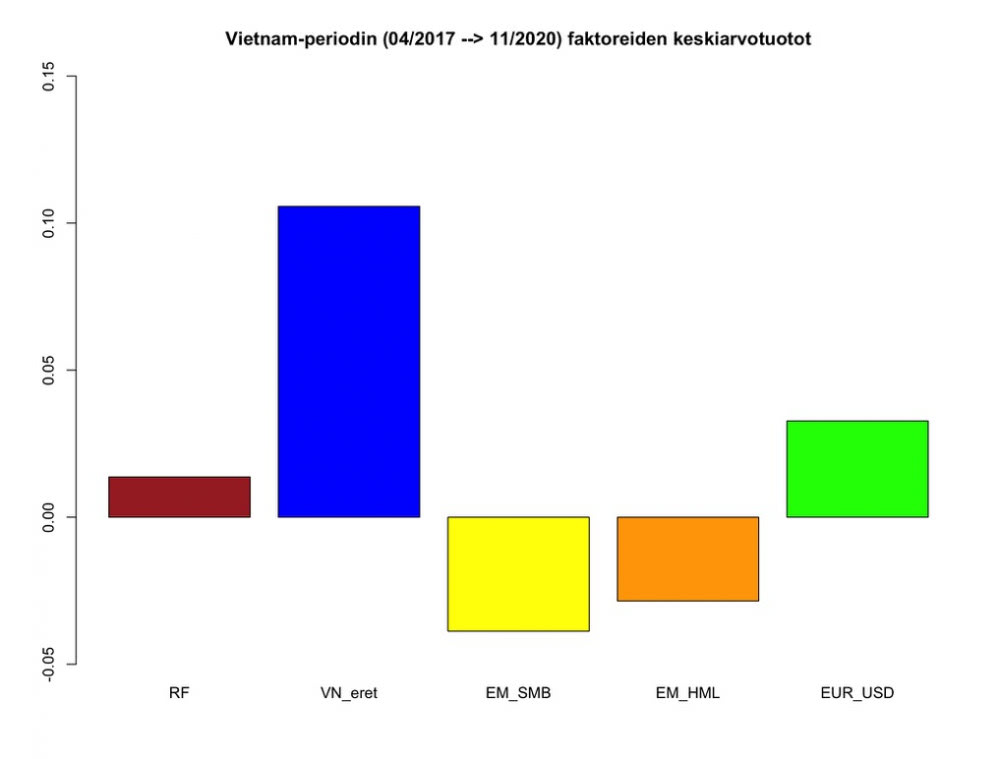Seuraavaksi PYN Eliten tuotto ja sen komponentit Vietnam-periodilla. Alpha on kohtuullisen suuri, mutta se koostunee pitkälti PYN Eliten osingoista. Smallcap ja value -altistukset ovat olleet tappiollisia. Vietnam indeksi on suurin komponentti. Valuuttakurssitappio on onnistuttu torjumaan lähes täysin.

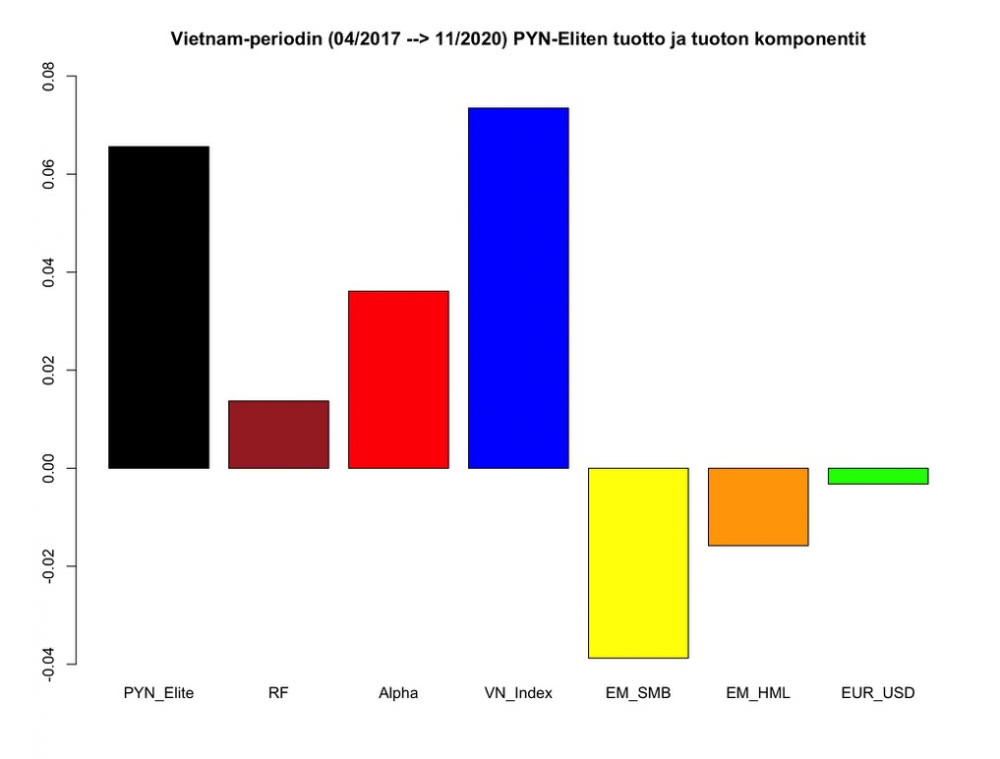Vietnam periodin tuotot (kuten koko Thaimaan jälkeisen periodinkin) näyttävät pitkälti muodostuvan altistuksesta Vietnamin pörssimarkkinalle sekä smallcap valuen tuotoille. Muodostin siksi kokeeksi kuvitteellisen rahaston (VN_SMB_HML_fund), joka altistuu saman verran noille kyseisille faktoreille kuin PYN Elite on altistunut. Alla kuva, jossa näkyy PYN Eliten, kuvitteellisen faktor-rahaston, size-faktorin sekä value-faktorin tuotto. Kuvasta nähdään, että PYN Elite korreloi hyvin, mutta ei täydellisesti kuvitteellisen rahaston kanssa. Lisäksi nähdään, että kun osakemarkkina romahtaa (covid-19), niin kaikki osaketuotoille altistuneet romahtaa eli korrelaatio lähestyy yhtä.

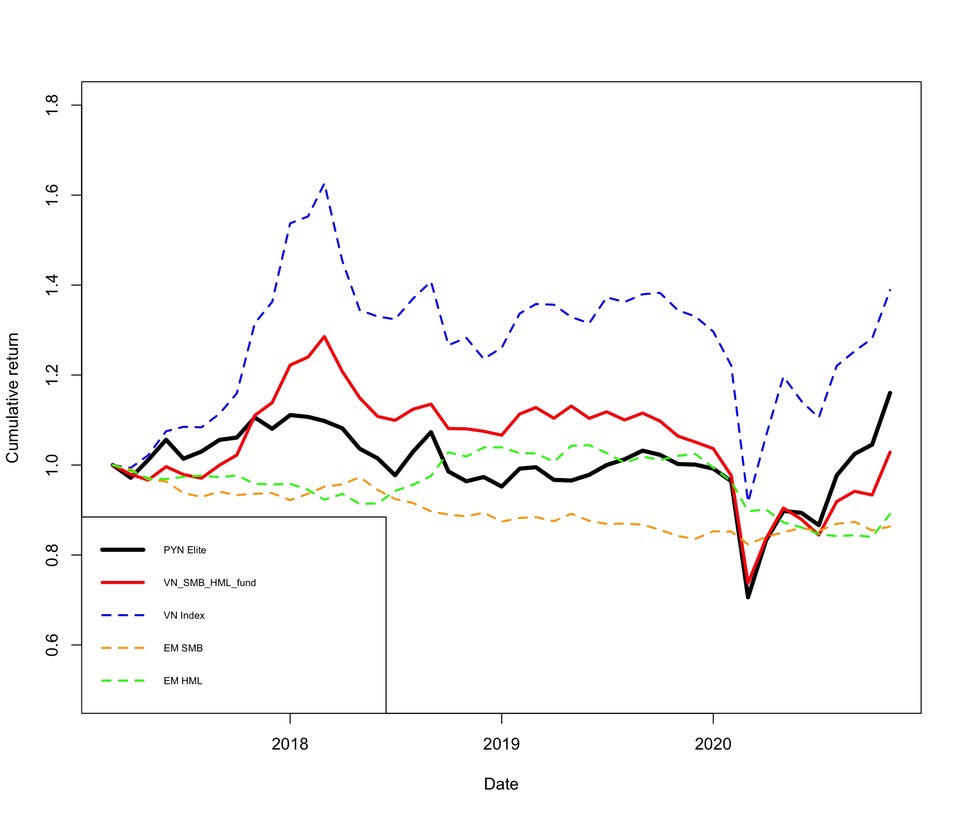Tässä alla vielä PYN Eliten tuotto selitettynä kuvitteellisen faktor-rahaston tuotoilla.

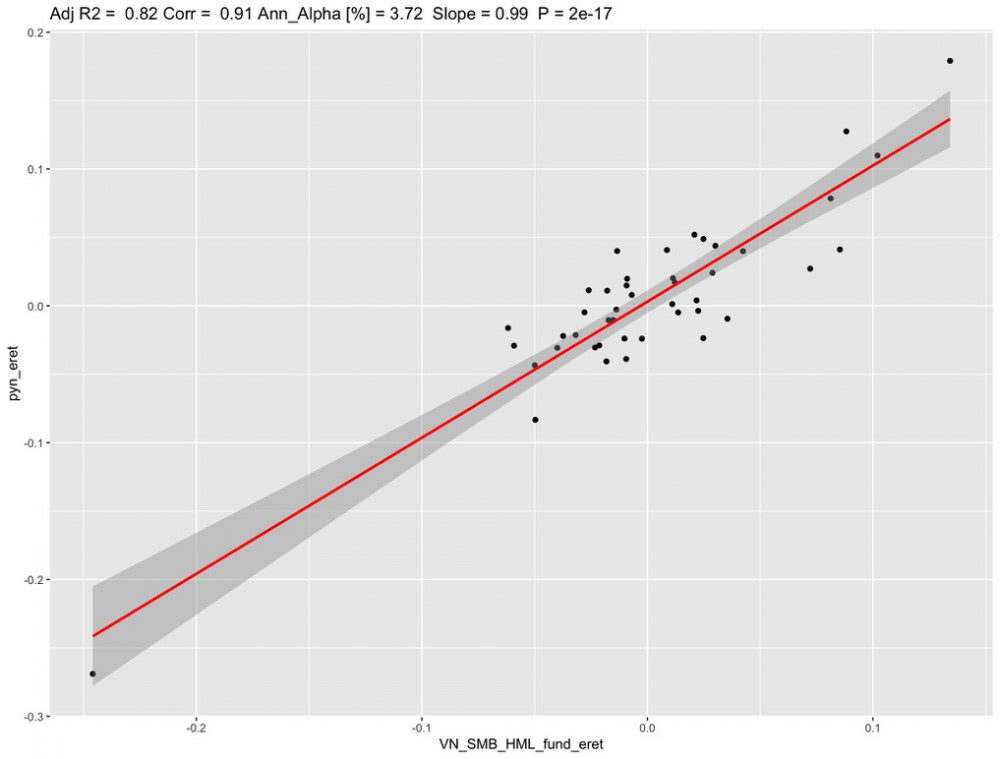
Yhteenveto

Yhteenvetona voidaan todeta, että puhtaasti kvantitatiivisen analyysin perusteella Thaimaa periodilla tuotot muodostuivat altistuksesta voimakkaasti nousevalle Thaimaan pörssimarkkinalle sekä selittämättömästä tuotosta eli alphasta. Thaimaan jälkeisellä periodilla tuotto on pääosin muodostunut altistuksesta Vietnamin osakemarkkinalle sekä smallcap value altistuksesta. Vietnamin aikana ylituoton tekeminen osakepoiminnalla vaikuttaa huomattavasti Thaimaa-aikaa vaikeammalta. Paras arvaukseni on, että rahaston kasvanut koko tuo ongelmansa alphan saalistuksessa. Suurempi pääoma vaatii sijoituksia microcap-yhtiöitä suurempiin yhtiöihin, jotka ovat tehokkaammin hinnoiteltuja? 

Näyttää siltä, että makrotason päätökset, erityisesti kohdemarkkinan valinta ja ajoitus ovat olleet merkittävimmät tekijät PYN Eliten menestyksessä. Mikrotason valinnat (erityisesti osakepoiminta markkinalla) näyttää olevan pienemmässä roolissa kuin altistuminen voimakkaasti nousevalle osakemarkkinalle. Kvantitatiivinen analyysi, joka mittaa alphaa, eli mikrotason selittämätöntä tuottoa, ei siis pysty mittaamaan aktiivisesti makrotason valintoja tekevän rahaston tai rahastonhoitajan taitoa kokonaisuudessaan.

Riippumatta mahdollisesta alphasta tai sen puutteesta, olen tyytyväinen PYN Eliten tuomaan altistukseen muiden (erityisesti Suomen) markkinoiden kanssa vain vähän korreloivaan Vietnamin osakemarkkinaan. Vietnamin markkinan suhteellisen maltillinen arvostus on plussaa. Otan myös mielellään vastaan kehittyvien markkinoiden smallcap value altistuksen. Value erityisesti on halpaa suhteessa historiaan. Bonuksena on salkunhoitajan selkeä tyyli ja rohkeus hakea arvoa potentiaalia omaavilta markkinoilta.

Bingo53 kirjoitti:

Itselläni kysymys koskee yllä mainittua, erittain laajasti hajautettua (VGWL:ssä on yli 3000 osaketta ympäri maailmaa) passiivista osakerahastoa ja sitä onko riski siinä niin pieni, että se jo itsessään korvaa riskittömän bondituotteen salkussa.

Täydelliselläkään hajautuksella ei saa poistettua osakkeiden markkinariskiä (systemaattinen riski). Eli siinä mielessä osakerahastolla ei voi korvata riskitöntä korkoa tai muita vähäriskisiä bondeja vaikka kuinka hajauttaisi. Toki on mahdollista pitää esim. 100% varoista allokoituna hajautettuun osakerahastoon, jos sietää osakkeiden markkinariskin täysimääräisenä. Eli siinä mielessä bondeja/riskitöntä korkoa ei välttämättä tarvita salkun komponenttina.

Kun käyttää Sharpe ratiota ja volatiliteettia (keskihajonta), niin kannattaa käyttää pitkiä aikasarjoja. Osaketuotot on tunnetusti paksuhäntäisiä eli pitkänkin ajan kestänyt korkea Sharpe ja/tai matala vola muuttuu kun häntäriski realisoituu ja markkina tippuu nopeasti paljon. Kymmenen tai mielellään kymmenien vuosien data antaa jo kohtuu luotettavan kuvan mitä parametrit ovat todellisuudessa historiassa olleet, mutta sekään ei tietysti takaa että samat parametrit pätee tulevaisuudessa.

Esimerkkinä voidaan laskea value weighted USAn osakemarkkinalle ja Buffettin Berkshire Hathawaylle Kellyn avulla joitain tunnuslukuja.

Data (Nov 1976 - Dec 2011) on Buffett's Alpha tutkimuksesta: http://docs.lhpedersen.com/BuffettsAlpha.pdf 

USAn osakemarkkina / Bershire Hathaway:

Aritmeettinen excess tuotto:      6.1% / 19.0%

Volatiliteetti:                                  15.8% / 24.9%

Sharpe ratio:                                    0.386 / 0.763

Geometrinen excess tuotto voidaan approksimoida (kaava 8) kun f=1: geom. excess tuotto = arit. excess tuotto - s^2/2:

Geometrinen excess tuotto:       4.9% / 15.9%

Näillä parametreilla voidaan laskea:

Maksimisijoitusaste f* = SR/s:                           2.44 / 3.06

Maksimi (f=f*) geom. excess tuotto SR^2/2:   7.5% / 29.1%

Geom. excess tuotto kun f=1: fs(SR-fs/2):       4.9% / 15.9%  (nämä vastaa yläpuolella approksimoituja arvoja)

Portfolion Kelly-paino c = s/SR:                        0.41 / 0.33

Eli USAn markkinan maksimisijoitusaste (full Kelly allokaatio) 1976-2011 oli 2.44 kun se Berkshirellä oli 3.06. Ei kovin suurta eroa. Eroa sen sijaan on teoreettisessa portfolion excess kasvunopeudessa maksimisijoitusasteella. Markkinan maksimikasvunopeus riskittömän koron päälle on 7.5% kun se Berkshirellä on 29.1%. Markkinaportfolion Kelly-paino (kun f=1) on alle half-kellyn (0.41). Berkshiren Kelly-paino on 1/3 Kelly.

OP:n tavoite oli oppia ymmärtämään/mallintamaan optimaalinen varojen allokointi (osakkeet/riskitön korko -suhde) portfolion kasvun kannalta sisältäen vivun vaikutuksen. Olen viime aikoina viettänyt paljon aikaa tämän ongelman parissa, joten nostetaan tätä vanhaa viestiketjua.

Ongelmaksi Kelly-kriteerin soveltamisessa osakesijoituksiin tulee sekä osaketuottojakauman että sijoitusaikahorisontin jatkuva muoto verrattuna diskreettiin vedonlyöntimaailmaan. Onneksemme viisaammat ovat ratkaisseet tämän ongelman ja tehneet Kellystä sovelluksen osakesijoittamiseen. Paras paperi, minkä olen aiheesta löytänyt, on Ed Thorpin (Thorp on Kellyn soveltamisen, optiohinnoittelun ja markkinaneutraalien hedge-fundien pioneeri) käsialaa ja löytyy esim. täältä: http://www.eecs.harvard.edu/cs286r/courses/fall12/papers/Thorpe_KellyCriterion2007.pdf (kappale 7. Wall street: the biggest game).

Innostuin tuosta Thorpin paperista siinä määrin, että kirjoitin graduni sen pohjalta soveltaen Kelly-kriteeriä osakehajautuksen vaikutusten arvioimiseen reaalisessa jatkuvan ajan maailmassa (geometristen keskiarvotuottojen maailma) teoreettisen Markowitzin single period maailman (aritmeettisten keskiarvotuottojen maailma) sijaan.

Gradu löytyy täältä: http://urn.fi/URN:NBN:fi:oulu-202011203162. 

Kelly-kriteeriä käsittelevä teoreettinen osuus on kappaleessa 3.3.4 Kelly criterion and the magic of Sharpe ratio. Kelly-kriteerin perustana toimiva geometrisen excess keskiarvotuoton kaava (sisältäen sijoitusasteen vaikutuksen) on johdettu useammalla eri tavalla kappaleessa 3.2 Derivation of the instantaneous geometric risk premium. Geometric risk premium on yhtä kuin geometrinen excess keskiarvotuotto tarkoittaen riskittömän koron ylittävää geometrista keskiarvotuottoa. Epiirisesti (kuukausittaista CRSP osakedataa käyttäen periodilla Jan/1973 - Jun/2018) (fractional) Kelly-kriteeri testataan kappaleessa 5.1 Fractional Kelly criterion explaining geometric risk premium.

Kaiken perusta on geometrisen risk premiumin (RP) eli geometrisen excess tuoton kaava (kaava 8):

RP = f(m – r) – (f^2s^2)/2

f on sijoitusaste eli portfoliosta osuus f on osakkeissa ja 1 – f riskittömässä korossa (esim. f=1 tarkoittaa 100% osakkeissa, 0% riskittömässä korossa).

m on portfolion aritmeettinen keskiarvotuotto (continuous compounding muodossa). 

r on riskitön korko (continuous compounding muodossa).

s on portfolion excess tuoton volatitiliteetti ja s^2 varianssi (gradussa tämä merkitään s subscriptillä e). Volatiliteetti lasketaan portfolion logaritmisista excess tuotoista eli kyseessä on tarkalleen ottaen excess kasvunopeuden standard deviaatio SD(ln(1+excess_ret)).

(Gradussa merkitsen excess tuoton: m subscriptillä e = m – r).

Kaavasta on helppo nähdä, että variance-drag -komponentti pienentää geometrista tuottoa ja, erityisesti, että sijoitusasteen neliö skaalaa variance-dragia. Kun mennään vivulle (f > 1), niin variance-drag alkaa nopeasti dominoida geometrista tuottoa ja ajaa sen helposti negatiiviseksi (johtaen ruiniin pitkällä aikavälillä). Koska hajauttaminen pienentää portfolion varianssia, mutta ei vaikuta aritmeettiseen keskiarvotuottoon m, on helppo nähdä, että hajauttaminen nostaa portfolion geometrisen tuoton odotusarvoa. Gradun keskeinen johtopäätös onkin, että oikeassa elämässä (kun sijoitusmenestystä mitataan geometrisilla tuotoilla) hajauttaminen on negatiivisen hinnan lounas, kun Markowitzin teoreettisessa single period elämässä se on ”vain” ilmainen lounas.

Osakesijoittamisen jatkuvassa maailmassa Kelly-kriteeri johdetaan derivoimalla edellinen kaava f:n suhteen (kaava 62):

f* = (m – r)/s^2

f* on full Kelly eli maksimaalisen portfolion kasvunopeuden odotusarvon tuottava sijoitusaste.

Teoreettinen Kelly-kriteeri olettaa, että portfolio rebalansoidaan jatkuvasti eli äärettömän nopealla tahdilla. Rebalansoinnissa osakepaino palautetaan targettiin f (ja lisäksi jos on esim. equally weighted portfolio, niin osakkeiden väliset painot palautetaan tasapainoihin). Tämä äärettömän tieheä rebalansointi takaa (koska portfolion arvonmuutokset lähestyvät äärettömän pientä per period), että portfolio ei suurellakaan vivulla koskaan mene yli 100% pakkaselle, jolloin meille jäisi kasvunopeutta laskettaessa negatiivinen luku logaritmin sisälle (tämä oli ymmärtääkseni yksi OP:n ongelmista)). Oikeassa elämässä tietysti joudutaan tyytymään ääretöntä pienempään rebalansointitaajuuteen (gradun empiirisessä osuudessa käytän kuukausittaista rebalansointia), mikä tarkoittaa (erityistesti huomioiden empiiristen tuottojakaumien paksut hännät), että empiirinen f* jää hieman teoreettista f* pienemmäksi.

Lisäksi teoreettinen Kelly-kriteeri olettaa, että vivuttava sijoittaja saa lainaa riskittömällä korolla. Tämä ei tietysti pidä paikkaansa oikeassa elämässä ja on yksi syy miksi Kellyn antama optimaalinen osakepaino f* on yliarvio. Oikeassa elämässä f* kannattaa ajatella teoreettisena ylärajana mieluummin kuin käytännöllisenä optimina.

Tulevaisuus on tietysti ennustamaton eli me ei tiedetä mitkä Kelly-kriteerin parametrit on esim. seuraavan 20 vuoden aikana. Tämä on yksi lisäargumentti, miksi on vaarallista luottaa sokeasti historiallisilla parametreilla laskettuun f* arvoon.

Kelly & Sharpe

Kuten kappaleen 3.3.4 nimi antaa ymmärtää, Sharpe ratio näyttelee suurta roolia geometrisen excess tuoton muodostumisessa. Thorp johtaa tämän omassa paperissaan, mutta toteaa asian lyhyesti vain kerran ja ikään kuin ohimennen. Minä tartuin tuohon Sharpe ratioon ja rakensin graduani pitkälti sen ympärille.

Sharpe ratio (tarkalleen ottaen instantaneous Sharpe ratio) on:

SR = (m-r)/s

m, r ja s ovat kuten edellä määriteltiin eli continuous compounding muodossa. Perinteinen Sharpe ratio lasketaan vuosittaisista tuotoista (ei siis continuos compounding) ja lisäksi s on perinteisesti yleensä aritmeettisen excess tuoton (logaritmisen excess tuoton sijaan) volatiliteetti. Käytännössä kuitenkin instantaneous Sharpe ration ja perinteisen Sharpe ration ero on hyvin pieni eikä sillä ole käytännön merkitystä. Tärkeää on kuitenkin käyttää aritmeettisia keskiarvotuottoja eikä geometrisia keskiarvotuottoja kuten usein näkee käytettävän.

Sharpe ratio voidaan Kellyn sääntöjen mukaan kirjoittaa myös näin:

SR = f*s (kaava 71) tai toisin sanoen f* = SR/s

Eli Sharpe ratio on yhtä kuin maksimisijoitusaste kertaa portfolion volatiliteetti eli Sharpe on yhtä kuin maksimiriski (volatiliteetti full Kelly pisteessä), jota sijoittajan ei tulisi koskaan ylittää. Esimerkiksi jos portolion Sharpe on 0.4 ja vola 0.2, niin maksimisijoitusaste f* = 2 = 200% osakkeissa.

Lisäksi portfolion Sharpe ratio määrittää myös maksimituoton (mitattuna geometrisena excess tuottona eli geometrisena risk premiumina) (kaava 66):

Max(RP) = SR^2/2

RP on geometrinen risk premium (eli g – r, jossa g on geometrinen keskiarvotuotto continuous compounding muodossa).

Eli portfolion maksimikasvunopeus sijoitusasteella f* on SR^2/2 + r.

Esimerkiksi jos SR on 0.4, vola 0.2 ja r on 0 niin saadaan (sijoitusasteella f* = 2 = 200% osakkeissa) 0.4^2/2 + 0 = 0.08 = 8%.

Geometrinen risk premium sijoitusasteen f funktiona saadaan (kaava 73):

RP(f) = fs(SR - fs/2)

Eli portfolion kasvunopeus sijoitusasteen funktiona on fs(SR - fs/2) + r.

Esimerkiksi jos SR on 0.4, vola 0.2 ja r on 0 niin saadaan 100% sijoitusasteella 1*0.2(0.4 – 1*0.2/2) + 0 = 0.06 = 6%. Tässä esimerkissä 100% sijoitusaste vastaa ns. half-Kellyä, joka tunnetusti tuottaa ¾ maksimituotosta (full Kellyn tuotosta) ½ riskillä (kun riskiä mitataan volalla).

Teoreettinen fractional Kellyn tuotto suhteessa full Kellyn tuottoon on kuvattu Kelly-painon c funktiona gradun kuvassa 2. c = f/f* eli sijoitusasteen f suhteellinen osuus full Kelly sijoitusasteesta f*. Full Kelly on siis kohdassa c = 1, jolloin half Kelly on kohdassa c = 0.5 jne. Kuvasta nähdään, että half Kelly tuottaa ¾ full Kellyn tuotosta. Samoin nähdään, että kun c = 2 niin osakkeet tuottavat odotusarvoisesti saman kuin riskitön korko (nollakohta on riskittömän koron tuotto). Kun c > 2 niin osakeriskin kantaminen johtaa odotusarvoisesti pienempään geometriseen tuottoon kuin sijoittaminen riskittömään korkoon. Kun c < 0 niin ollaan shorttina osakkeisiin. Rationaalinen Kelly-paino c on siis nollan ja yhden välillä riippuen sijoittajan preferensseistä.

Portfolion Kelly-paino sijoitusasteen funktiona saadaan: 

c = fs/SR (kaava 72)

Sijoittamalla f=1, minkä tahansa portfolion Kelly-paino c voidaan laskea yksinkertaisesti jakamalla portfolion vola portfolion Sharpella. Tämä on kätevä ja yksinkertainen tapa määrittää portfolion riskitaso.

Geometrinen risk premium voidaan esittää myös Kelly-painon c funktiona, jolloin ei tarvita mitään muita parametreja Kelly-painon lisäksi kuin Sharpe ratio:

RP(c) = c(1-c/2)SR^2 (kaava 69)

Eli portfolion kasvunopeus Kelly-painon c funktiona on c(1-c/2)SR^2 + r.

USAn historialliset osakemarkkinatuotot ja fractional Kelly

Se teoreettisista esimerkeistä. Mutta miten tämä teoria toimii empiirisellä datalla testattuna? Vastaus on, että hämmästyttävän hyvin. Tai ehkä sen ei pitäisi olla hämmästyttävää huomioiden, että me testataan erittäin suurella datalla (lähes 3 miljoonaa yksittäistä osakkeiden kuukausituottoa, joista muodostetaan satunnaisesti kuukausittain 50 000 portfoliota 45.5 vuoden ajalta) ”matemaattista lakia” eli geometrisen excess keskiarvotuoton kaavaa (kaava 8). Sample size on riittävä, jotta suurten lukujen laki tekee tehtävänsä ja geometrinen excess keskiarvotuotto konvergoituu odotusarvoonsa (pois lukien suurella vivulla, jossa empiirinen tuotto alkaa systemaattisesti jäädä teoreettisesta ennusteesta).

Kuvassa 13 nähdään kaavoista ennustettu geometrinen risk premium (Predicted) ja empiirisestä datasta todennettu tulos (Bootstrapped) aikavälillä Jan/1973 - Jun/2018. Empiiriset tulokset muodostuvat 50 000 kuukausittain satunnaisesti valitusta portfoliosta per portfoliokoko sekä kaikki osakkeet sisältävästä benchmark portfoliosta. X-akselilla on sijoitusaste f. Kaikki portfoliot ovat equally weighted ja kuukausittain rebalansoitu. Equal weightinginstä johtuen microcap osakkeet dominoi tuloksia. Kuvat 14-16 sisältävät vastaavat tulokset microcap, small stocks ja big stocks kategorioille eriteltynä. 

Kuvasta 13 nähdään, että täysin hajautetun equally weighted benchmark portolion full Kelly piste on yli 2 (teoreettinen 2.36 ja empiirinen 2.16). Lisäksi nähdään, että empiiriset käyrät seuraavat varsin tarkasti ennusteita, kunnes suurella vivulla (erityisesti 1.5 jälkeen) empiiriset tulokset alkavat jäädä ennustetuista. Tämä ero liittyy paksuhäntäisiin tuottoihin yhdistettynä epäoptimaaliseen rebalansointitaajuuteen (kuukausittainen rebalansointi on liian harva suurella vivulla).

Lisäksi kuvasta 13 näkyy hajautuksen merkitys. 100% osakeallokaatiolla benchmark portfolion realisoitunut geometrinen excess keskiarvotuotto on vajaa 8% per annum. Yhden osakkeen portfoliolle keskiarvotuotto jää noin -7% paikkeille. Ero on lähes 15 prosenttiyksikköä. 10 osakkeen portfoliolla tappiota benchmarkille jää noin 1.6 prosenttiyksikköä per annum. Ero (hajautuksen merkitys) korostuu mitä suurempi sijoitusaste on. Vaikka microcap painotteinen equally weighted benchmark ei ole täysin implementoitavissa (johtuen microcappien epälikvidiydestä), on selvää, että hajauttaminen on negatiivisen hinnan lounas. Hajauttamalla enemmän saa sekä alemman riskin että suuremman geometrisen keskiarvotuoton.

Kuvassa 17 näkyy erittäin heikosti hajautettujen portfolioiden (1-5 osaketta) geometriset risk premiumit sijoitusasteen funktiona. Huomionarvoista on, että aina kun portfolio koostuu viidestä tai alle viidestä osakkeesta niin 100% osakeallokaatio tuottaa alemman (geometrisen) risk premiumin kuin jokin alempi osakeallokaatio tuottaisi. Esimerkiksi yhden osakkeen portfolio saavuttaa maksimituoton 29% osakeallokaatiolla (71% riskittömässä korossa). Lisäksi näemme, että yhden osakkeen portfolio tuottaa odotusarvoisesti huomattavasti alle riskittömän koron 100% osakeallokaatiolla. Kahden osakkeen portfolio tuottaa odotusarvoisesti melko tarkasti saman kuin riskitön korko.

Bottom line

Sijoittaja tarvitsee vain estimaatin portfolion Sharpe ratiosta ja volatiliteetista. Näiden avulla saadaan helposti laskettua estimaatti portfolion Kelly-pisteelle (eli maksimivivulle), maksimikasvunopeudelle tai kasvunopeudelle millä tahansa sijoitusasteella. Toisin sanoen Sharpe ratio ja volatiliteetti riittävät määrittämään sijoittajan koko mahdollisuuksien kirjon (opportunity set). Tuosta mahdollisuuksien kirjosta sijoittaja voi valita itselleen sopivan riskitason ja saada sitä vastaavan portfolion odotusarvoisen kasvutahdin.